|
General The factorials and binomials have a very long history connected with their natural appearance in combinatorial problems. Such combinatorial‐type problems were known and partially solved even in ancient times. The first mathematical descriptions of binomial coefficients arising from expansions of 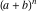 for for  appeared in the works of Chia Hsien (1050), al-Karaji (about 1100), Omar al-Khayyami (1080), Bhaskara Acharya (1150), al‐Samaw'al (1175), Yang Hui (1261), Tshu shi Kih (1303), Shih–Chieh Chu (1303), M. Stifel (1544), Cardano (1545), Scheubel (1545), Peletier (1549), Tartaglia (1556), Cardan (1570), Stevin (1585), Faulhaber (1615), Girard (1629), Oughtred (1631), Briggs (1633), Mersenne (1636), Fermat (1636), Wallis (1656), Montmort (1708), and De Moivre (1730). B. Pascal (1653) gave a recursion relation for the binomial, and I. Newton (1676) studied its cases with fractional arguments. appeared in the works of Chia Hsien (1050), al-Karaji (about 1100), Omar al-Khayyami (1080), Bhaskara Acharya (1150), al‐Samaw'al (1175), Yang Hui (1261), Tshu shi Kih (1303), Shih–Chieh Chu (1303), M. Stifel (1544), Cardano (1545), Scheubel (1545), Peletier (1549), Tartaglia (1556), Cardan (1570), Stevin (1585), Faulhaber (1615), Girard (1629), Oughtred (1631), Briggs (1633), Mersenne (1636), Fermat (1636), Wallis (1656), Montmort (1708), and De Moivre (1730). B. Pascal (1653) gave a recursion relation for the binomial, and I. Newton (1676) studied its cases with fractional arguments. It was known that the factorial 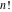 grows very fast. Its growth speed was estimated by J. Stirling (1730) who found the famous asymptotic formula for the factorial named after him. A special role in the history of the factorial and binomial belongs to L. Euler, who introduced the gamma function grows very fast. Its growth speed was estimated by J. Stirling (1730) who found the famous asymptotic formula for the factorial named after him. A special role in the history of the factorial and binomial belongs to L. Euler, who introduced the gamma function 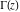 as the natural extension of factorial ( as the natural extension of factorial (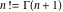 ) for noninteger arguments and used notations with parentheses for the binomials (1774, 1781). C. F. Hindenburg (1779) used not only binomials but introduced multinomials as their generalizations. The modern notation ) for noninteger arguments and used notations with parentheses for the binomials (1774, 1781). C. F. Hindenburg (1779) used not only binomials but introduced multinomials as their generalizations. The modern notation 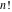 was suggested by C. Kramp (1808, 1816). C. F. Gauss (1812) also widely used binomials in his mathematical research, but the modern binomial symbol was suggested by C. Kramp (1808, 1816). C. F. Gauss (1812) also widely used binomials in his mathematical research, but the modern binomial symbol 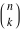 was introduced by A. von Ettinghausen (1826); later Förstemann (1835) gave the combinatorial interpretation of the binomial coefficients. was introduced by A. von Ettinghausen (1826); later Förstemann (1835) gave the combinatorial interpretation of the binomial coefficients. A. L. Crelle (1831) used a symbol that notates the generalized factorial 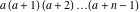 . Later P. E. Appell (1880) ascribed the name Pochhammer symbol for the notation of this product because it was widely used in the research of L. A. Pochhammer (1890). . Later P. E. Appell (1880) ascribed the name Pochhammer symbol for the notation of this product because it was widely used in the research of L. A. Pochhammer (1890). While the double factorial 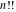 was introduced long ago, its extension for complex arguments was suggested only several years ago by J. Keiper and O. I. Marichev (1994) during the implementation of the function Factorial2 in Mathematica. was introduced long ago, its extension for complex arguments was suggested only several years ago by J. Keiper and O. I. Marichev (1994) during the implementation of the function Factorial2 in Mathematica. The classical combinatorial applications of the factorial and binomial functions are the following: 57181644131429Item613418010943441Item723121614745161Item
|