|
Introduction to the Fresnel integrals
General
The Fresnel integrals appeared in the works by A. J. Fresnel (1798, 1818, 1826) who investigated an optical problem. Later K. W. Knochenhauer (1839) found series representations of these integrals. N. Nielsen (1906) studied various properties of these integrals.
Different authors used the same notations  and and  , but with slightly different definitions. , but with slightly different definitions.
Definitions of Fresnel integrals
The Fresnel integrals 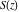 and and 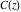 are defined as values of the following definite integrals: are defined as values of the following definite integrals:
A quick look at the Fresnel integrals Here is a quick look at the graphics for the Fresnel integrals along the real axis. The parametrically described curve  with with 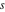 ranging over a subset of the real axis gives the following characteristic spiral. ranging over a subset of the real axis gives the following characteristic spiral.
Connections within the group of Fresnel integrals and with other function groups
Representations through more general functions
The Fresnel integrals 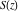 and and 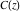 are particular cases of the more general functions: hypergeometric and Meijer G functions. are particular cases of the more general functions: hypergeometric and Meijer G functions.
For example, they can be represented through regularized hypergeometric functions 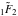 : :
These two integrals can also be expressed through generalized and classical Meijer G functions:
The first two formulas are simpler than the last two classical representations (which include factors like 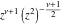 ). ).
Representations through related equivalent functions
The Fresnel integrals  and and 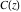 can be represented through a combination of probability integrals can be represented through a combination of probability integrals 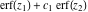 with corresponding values of with corresponding values of 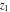 , , 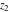 , and , and  : :
The best-known properties and formulas for Fresnel integrals
Real values for real arguments
For real values of argument 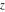 , the values of the Fresnel integrals , the values of the Fresnel integrals  and and 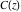 are real. are real.
Simple values at zero and infinity
The Fresnel integrals 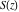 and and 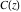 have simple values for arguments have simple values for arguments  and and 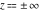 : :
Analyticity
The Fresnel integrals 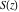 and and 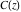 are defined for all complex values of are defined for all complex values of 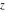 , and they are analytical functions of , and they are analytical functions of 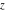 over the whole complex over the whole complex 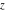 ‐plane and do not have branch cuts or branch points. They are entire functions with an essential singular point at ‐plane and do not have branch cuts or branch points. They are entire functions with an essential singular point at 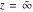 . .
Periodicity
The Fresnel integrals 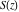 and and 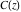 do not have periodicity. do not have periodicity.
Parity and symmetry
The Fresnel integrals 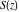 and and 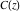 are odd functions and have mirror symmetry: are odd functions and have mirror symmetry:
Series representations
The Fresnel integrals 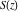 and and 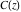 have rather simple series representations at the origin: have rather simple series representations at the origin:
These series converge at the whole 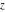 ‐plane and their symbolic forms are the following: ‐plane and their symbolic forms are the following:
Interestingly, closed-form expressions for the truncated version of the Taylor series at the origin can be expressed through the generalized hypergeometric function 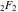 , for example: , for example:
Asymptotic series expansions
The asymptotic behavior of the Fresnel integrals 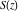 and and 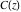 can be described by the following formulas (only the main terms of asymptotic expansion are given): can be described by the following formulas (only the main terms of asymptotic expansion are given):
The previous formulas are valid in any directions of approaching point 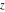 to infinity ( to infinity (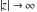 ). In particular cases when ). In particular cases when 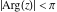 and and 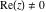 , the formulas can be simplified to the following relations: , the formulas can be simplified to the following relations:
Integral representations
The Fresnel integrals 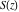 and and  have the following simple integral representations through sine or cosine that directly follow from the definition of these integrals: have the following simple integral representations through sine or cosine that directly follow from the definition of these integrals:
Transformations
The argument of the Fresnel integrals 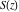 and and 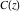 with square root arguments can sometimes be simplified: with square root arguments can sometimes be simplified:
Simple representations of derivatives
The derivatives of the Fresnel integrals 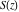 and and 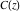 are the sine or cosine functions with simple arguments: are the sine or cosine functions with simple arguments:
The symbolic derivatives of the 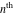 order have the following representations: order have the following representations:
Simple of differential equations
The Fresnel integrals 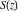 and and 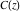 satisfy the following third-order linear ordinary differential equation: satisfy the following third-order linear ordinary differential equation:
They can be represented as partial solutions of the previous equation under the following corresponding initial conditions:
Applications of Fresnel integrals
Applications of Fresnel integrals include Fraunhofer diffraction, asymptotics of Weyl sums, and railway and freeway constructions.
|