|
General
The gamma function 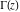 is used in the mathematical and applied sciences almost as often as the well-known factorial symbol is used in the mathematical and applied sciences almost as often as the well-known factorial symbol  . It was introduced by the famous mathematician L. Euler (1729) as a natural extension of the factorial operation . It was introduced by the famous mathematician L. Euler (1729) as a natural extension of the factorial operation 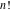 from positive integers from positive integers 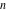 to real and even complex values of the argument to real and even complex values of the argument 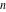 . This relation is described by the following formula: . This relation is described by the following formula:
L. Euler derived some basic properties and formulas for the gamma function. He started investigations of  from the infinite product from the infinite product
and the integral
which is currently known as the beta function integral. As a result, Euler derived the following integral representation for factorial  : :
which can be easily converted into the well-known Euler integral for the gamma function:
Also, during his research, Euler closely approached the famous reflection formula:
which later got his name.
At the same time, J. Stirling (1730) found the famous asymptotic formula for the factorial, which bears his name. This formula was also naturally applied to the gamma function resulting in the following asymptotic relation:
Later, A. M. Legendre (1808, 1814) suggested the current symbol Γ for the gamma function and discovered the duplication formula:
It was generalized by C. F. Gauss (1812) to the multiplication formula:
F. W. Newman (1848) studied the reciprocal of the gamma function and found that it is an entire function and has the following product representation valid for the whole complex plane:
where  is the Euler–Mascheroni gamma constant. is the Euler–Mascheroni gamma constant.
B. Riemann (1856) proved an important relation between the gamma and zeta functions:
which was mentioned centuries ago in an article by Euler (1749) for particular values of the argument 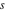 . .
K. Weierstrass (1856) and other nineteenth century mathematicians widely used the gamma function in their investigations and discovered many more complicated properties and formulas for it. In particular, H. Hankel (1864, 1880) derived its contour integral representation for complex arguments, and O. Hölder (1887) proved that the gamma function does not satisfy any algebraic differential equation. This result was subsequently re-proved by A. Ostrowski (1925).
Many mathematicians devote special attention to the question of the uniqueness of extending the factorial operation  from positive integers to arbitrary real or complex values. Evidently this question is connected to the solutions of the functional equation: from positive integers to arbitrary real or complex values. Evidently this question is connected to the solutions of the functional equation:
J. Hadamard (1894) found that the function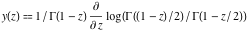 is an entire analytic function that coincides with is an entire analytic function that coincides with 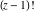 for for 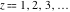 . But this function satisfies the more complicated functional equation . But this function satisfies the more complicated functional equation 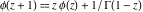 and has a more complicated integral representation than the classical gamma function defined by the Euler integral. and has a more complicated integral representation than the classical gamma function defined by the Euler integral.
H. Bohr and J. Mollerup (1922) proved that the gamma function  is the only function that satisfies the recurrence relationship is the only function that satisfies the recurrence relationship 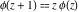 , is positive for , is positive for 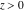 , equals one at , equals one at 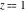 , and is logarithmically convex (that is, , and is logarithmically convex (that is, 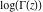 is convex). If the restriction on convexity is absent, then the recurrence relationship has an infinite set of solutions in the form is convex). If the restriction on convexity is absent, then the recurrence relationship has an infinite set of solutions in the form 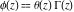 , where , where 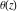 is an arbitrary periodic function with period is an arbitrary periodic function with period  . .
|