|
The gamma function 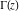 can be exactly evaluated in the points can be exactly evaluated in the points 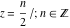 . Here are examples: . Here are examples:
The preceding evaluations can be provided by the formulas:
At the points 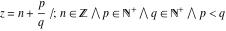 , the values of the gamma function , the values of the gamma function 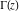 can be represented through values of can be represented through values of 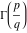 : :
For real values of argument 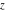 , the values of the gamma function , the values of the gamma function 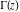 are real (or infinity). The gamma function is not equal to zero: are real (or infinity). The gamma function is not equal to zero:
The gamma function 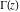 is an analytical function of is an analytical function of 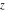 , which is defined over the whole complex , which is defined over the whole complex 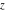 ‐plane with the exception of countably many points ‐plane with the exception of countably many points 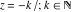 . The reciprocal of the gamma function . The reciprocal of the gamma function 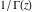 is an entire function. is an entire function.
The function 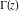 has an infinite set of singular points has an infinite set of singular points 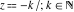 , which are the simple poles with residues , which are the simple poles with residues 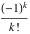 . The point . The point 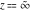 is the accumulation point of the poles, which means that is the accumulation point of the poles, which means that 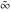 is an essential singular point. is an essential singular point.
The function 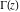 does not have branch points and branch cuts. does not have branch points and branch cuts.
The function 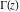 does not have periodicity. does not have periodicity.
The function 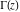 has mirror symmetry: has mirror symmetry:
The derivatives of 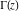 can be represented through gamma and polygamma functions: can be represented through gamma and polygamma functions:
The gamma function 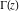 does not satisfy any algebraic differential equation (O. Hölder, 1887). But it is the solution of the following nonalgebraic equation: does not satisfy any algebraic differential equation (O. Hölder, 1887). But it is the solution of the following nonalgebraic equation:
Series representations of the gamma function 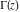 near the poles near the poles 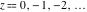 are of great interest for applications in the theory of generalized hypergeometric, Meijer G, and Fox H functions. These representations can be described by the formulas: are of great interest for applications in the theory of generalized hypergeometric, Meijer G, and Fox H functions. These representations can be described by the formulas:
where 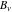 are the Bernoulli numbers. are the Bernoulli numbers.
Asymptotic behavior of the gamma function 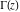 is described by the famous Stirling formula: is described by the famous Stirling formula:
This formula allows derivation of the following asymptotic expansion for the ratio of gamma functions:
The gamma function 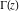 has several integral representations that are different from the Euler integral: has several integral representations that are different from the Euler integral:
and related integral
which can be used for defining the gamma function over the whole complex plane.
Some of the integral representations are the following:
This final formula is known as Hankel's contour integral. The path of integration 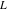 starts at starts at 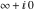 on the real axis, goes to on the real axis, goes to 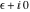 , circles the origin in the counterclockwise direction with radius , circles the origin in the counterclockwise direction with radius 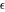 to the point to the point 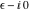 , and returns to the point , and returns to the point 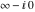 . .
The following infinite product representation for 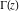 clearly illustrates that clearly illustrates that 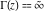 at at 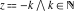 : :
The similar product representation for 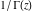 illustrates that illustrates that 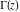 is an entire function: is an entire function:
The following famous limit representation for 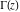 was known to L. Euler: was known to L. Euler:
It can be modified to the following related limit representations:
The gamma function can be evaluated as the limit of the following definite integral:
The most famous definite integrals, including the gamma function, belong to the class of Mellin–Barnes integrals. They are used to provide a uniform representation of all generalized hypergeometric, Meijer G, and Fox H functions. For example, the Meijer G function is defined as the value of the following Mellin–Barnes integral:
The infinite contour of integration 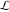 separates the poles of separates the poles of 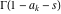 at at 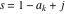 , , 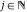 from the poles of from the poles of 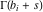 at at 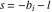 , , 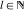 . Such a contour always exists in the cases . Such a contour always exists in the cases 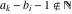 . .
There are three possibilities for the contour 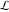 : :
(i) 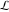 runs from γ-ⅈ∞ to γ+ⅈ∞ (where runs from γ-ⅈ∞ to γ+ⅈ∞ (where 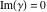 ) so that all poles of ) so that all poles of 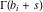 , , 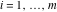 , are to the left of , are to the left of 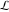 , and all the poles of , and all the poles of 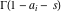 , ,  are to the right of ℒ. This contour can be a straight line are to the right of ℒ. This contour can be a straight line 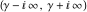 if if 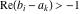 (then (then 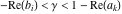 ). In this case, the integral converges if ). In this case, the integral converges if 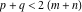 , , 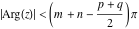 . If . If 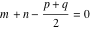 , then , then 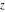 must be real and positive, and the additional condition must be real and positive, and the additional condition 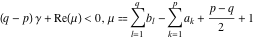 , should be added. , should be added.
(ii) 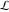 is a left loop, starting and ending at is a left loop, starting and ending at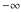 and encircling all poles of and encircling all poles of 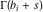 , ,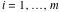 , once in the positive direction, but none of the poles of , once in the positive direction, but none of the poles of 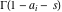 , , 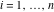 . In this case, the integral converges if . In this case, the integral converges if 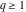 and either and either 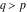 or or 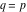 and and 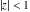 or or 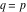 and and 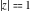 and and 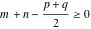 and and 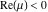 . .
(iii) 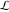 is a right loop, starting and ending at +∞ and encircling all poles of is a right loop, starting and ending at +∞ and encircling all poles of 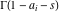 , , 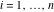 , once in the negative direction, but none of the poles of , once in the negative direction, but none of the poles of 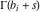 , , 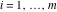 . In this case, the integral converges if . In this case, the integral converges if 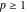 , and either , and either 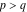 or or 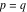 and and 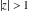 or or 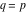 and and 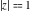 and and 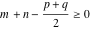 and and 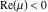 . .
In particular cases, the last integral can be evaluated using simpler elementary and special functions:
The definition of the Meijer G function through a Mellin‐Barnes integral realizes the inverse Mellin integral transform of ratios of gamma functions:
The contour 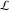 is the vertical straight line is the vertical straight line 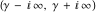 . It allows the writing of the following rather general formula for the inverse Mellin integral transform: . It allows the writing of the following rather general formula for the inverse Mellin integral transform:
In particular cases, it gives the following representations:
The following formulas describe some transformations of the gamma functions with linear arguments into expressions that contain the gamma function with the simplest argument:
In the case of multiple arguments 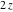 , , 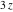 ,…, ,…, 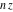 , the gamma function , the gamma function 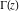 can be represented by the following duplication and multiplication formulas, derived by A. M. Legendre and C. F. Gauss: can be represented by the following duplication and multiplication formulas, derived by A. M. Legendre and C. F. Gauss:
The product of two gamma functions 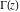 and and 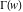 , with arguments satisfying the condition that , with arguments satisfying the condition that 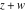 is an integer, can be represented through elementary functions: is an integer, can be represented through elementary functions:
The preceding formula transforms into the following formula and its relatives:
The ratio of two gamma functions 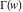 and and 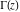 , with arguments satisfying the condition that , with arguments satisfying the condition that 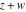 is integer, can be represented through a polynomial or rational function: is integer, can be represented through a polynomial or rational function:
The gamma function 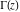 satisfies the following recurrence identities: satisfies the following recurrence identities:
These formulas can be generalized to the following recurrence identities with a jump of length 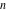 : :
The most famous inequalities for the gamma function can be described by the following formulas:
The gamma function is used throughout mathematics, the exact sciences, and engineering.
|