|
Introduction to the gamma functions
General
The gamma function 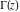 is applied in exact sciences almost as often as the well‐known factorial symbol is applied in exact sciences almost as often as the well‐known factorial symbol 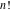 . It was introduced by the famous mathematician L. Euler (1729) as a natural extension of the factorial operation . It was introduced by the famous mathematician L. Euler (1729) as a natural extension of the factorial operation 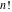 from positive integers from positive integers 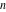 to real and even complex values of this argument. This relation is described by the formula: to real and even complex values of this argument. This relation is described by the formula:
Euler derived some basic properties and formulas for the gamma function. He started investigations of 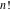 from the infinite product: from the infinite product:
The gamma function 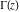 has a long history of development and numerous applications since 1729 when Euler derived his famous integral representation of the factorial function. In modern notation it can be rewritten as the following: has a long history of development and numerous applications since 1729 when Euler derived his famous integral representation of the factorial function. In modern notation it can be rewritten as the following:
The history of the gamma function is described in the subsection "General" of the section "Gamma function." Since the famous work of J. Stirling (1730) who first used series for 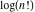 to derive the asymptotic formula for to derive the asymptotic formula for  , mathematicians have used the logarithm of the gamma function , mathematicians have used the logarithm of the gamma function 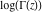 for their investigations of the gamma function for their investigations of the gamma function 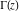 . Investigators of mention include: C. Siegel, A. M. Legendre, K. F. Gauss, C. J. Malmstén, O. Schlömilch, J. P. M. Binet (1843), E. E. Kummer (1847), and G. Plana (1847). M. A. Stern (1847) proved convergence of the Stirling's series for the derivative of . Investigators of mention include: C. Siegel, A. M. Legendre, K. F. Gauss, C. J. Malmstén, O. Schlömilch, J. P. M. Binet (1843), E. E. Kummer (1847), and G. Plana (1847). M. A. Stern (1847) proved convergence of the Stirling's series for the derivative of 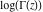 . C. Hermite (1900) proved convergence of the Stirling's series for . C. Hermite (1900) proved convergence of the Stirling's series for 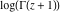 if if 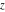 is a complex number. is a complex number.
During the twentieth century, the function log(Γ(z)) was used in many works where the gamma function was applied or investigated. The appearance of computer systems at the end of the twentieth century demanded more careful attention to the structure of branch cuts for basic mathematical functions to support the validity of the mathematical relations everywhere in the complex plane. This lead to the appearance of a special log‐gamma function 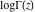 , which is equivalent to the logarithm of the gamma function , which is equivalent to the logarithm of the gamma function  as a multivalued analytic function, except that it is conventionally defined with a different branch cut structure and principal sheet. The log‐gamma function as a multivalued analytic function, except that it is conventionally defined with a different branch cut structure and principal sheet. The log‐gamma function 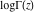 was introduced by J. Keiper (1990) for Mathematica. It allows a concise formulation of many identities related to the Riemann zeta function was introduced by J. Keiper (1990) for Mathematica. It allows a concise formulation of many identities related to the Riemann zeta function 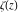 . .
The importance of the gamma function and its Euler integral stimulated some mathematicians to study the incomplete Euler integrals, which are actually equal to the indefinite integral of the expression 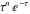 . They were introduced in an article by A. M. Legendre (1811). Later, P. Schlömilch (1871) introduced the name "incomplete gamma function" for such an integral. These functions were investigated by J. Tannery (1882), F. E. Prym (1877), and M. Lerch (1905) (who gave a series representation for the incomplete gamma function). N. Nielsen (1906) and other mathematicians also had special interests in these functions, which were included in the main handbooks of special functions and current computer systems like Mathematica. . They were introduced in an article by A. M. Legendre (1811). Later, P. Schlömilch (1871) introduced the name "incomplete gamma function" for such an integral. These functions were investigated by J. Tannery (1882), F. E. Prym (1877), and M. Lerch (1905) (who gave a series representation for the incomplete gamma function). N. Nielsen (1906) and other mathematicians also had special interests in these functions, which were included in the main handbooks of special functions and current computer systems like Mathematica.
The needs of computer systems lead to the implementation of slightly more general incomplete gamma functions and their regularized and inverse versions. In addition to the classical gamma function 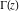 , Mathematica includes the following related set of gamma functions: incomplete gamma function , Mathematica includes the following related set of gamma functions: incomplete gamma function 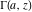 , generalized incomplete gamma function , generalized incomplete gamma function  , regularized incomplete gamma function , regularized incomplete gamma function  , generalized regularized incomplete gamma function , generalized regularized incomplete gamma function 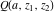 , log‐gamma function , log‐gamma function  , inverse of the regularized incomplete gamma function , inverse of the regularized incomplete gamma function 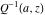 , and inverse of the generalized regularized incomplete gamma function , and inverse of the generalized regularized incomplete gamma function 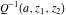 . .
Definitions of gamma functions
The gamma function  , the incomplete gamma function , the incomplete gamma function 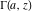 , the generalized incomplete gamma function , the generalized incomplete gamma function 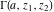 , the regularized incomplete gamma function , the regularized incomplete gamma function 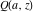 , the generalized regularized incomplete gamma function , the generalized regularized incomplete gamma function 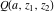 , the log‐gamma function (almost equal to the logarithm of the gamma function) , the log‐gamma function (almost equal to the logarithm of the gamma function)  , the inverse of the regularized incomplete gamma function , the inverse of the regularized incomplete gamma function 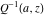 , and the inverse of the generalized regularized incomplete gamma function , and the inverse of the generalized regularized incomplete gamma function  are defined by the following formulas: are defined by the following formulas:
The function
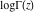
is equivalent to
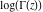
as a multivalued analytic function, except that it is conventionally defined with a different branch cut structure and principal sheet. The function
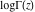
allows a concise formulation of many identities related to the Riemann zeta function
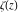
:
The previous functions comprise the interconnected group called the gamma functions.
Instead of the first three previous classical definitions using definite integrals, the other equivalent definitions with infinite series can be used.
A quick look at the gamma functions Here is a quick look at graphics for the gamma function and the function 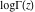 along the real axis. The real parts are shown in red and the imaginary parts are shown in blue. along the real axis. The real parts are shown in red and the imaginary parts are shown in blue. Here is a quick look at the graphics for the gamma function and the function 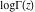 along the real axis. along the real axis. These two graphics show the real part (left) and imaginary part (right) of 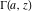 over the over the 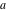 ‐ ‐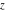 –plane. –plane. The next graphic shows the regularized incomplete gamma function 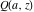 over the over the 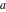 ‐ ‐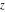 -plane. -plane.
Connections within the group of gamma functions and with other function groups
Representations through more general functions
The incomplete gamma functions 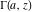 , , 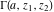 , , 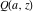 , and , and 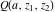 are particular cases of the more general hypergeometric and Meijer G functions. are particular cases of the more general hypergeometric and Meijer G functions.
For example, they can be represented through hypergeometric functions  and and 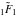 or the Tricomi confluent hypergeometric function or the Tricomi confluent hypergeometric function  : :
These functions also have rather simple representations in terms of classical Meijer G functions:
The log‐gamma function  can be expressed through polygamma and zeta functions by the following formulas: can be expressed through polygamma and zeta functions by the following formulas:
Representations through related equivalent functions
The gamma functions 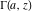 , , 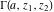 , , 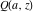 , and , and 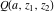 can be represented using the related exponential integral can be represented using the related exponential integral 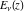 by the following formulas: by the following formulas:
Relations to inverse functions
The gamma functions 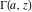 , , 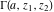 , , 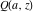 , and , and  are connected with the inverse of the regularized incomplete gamma function are connected with the inverse of the regularized incomplete gamma function 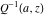 and the inverse of the generalized regularized incomplete gamma function and the inverse of the generalized regularized incomplete gamma function 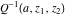 by the following formulas: by the following formulas:
Representations through other gamma functions
The gamma functions 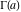 , , 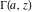 , , 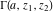 , ,  , , 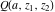 , and , and  are connected with each other by the formulas: are connected with each other by the formulas:
The best-known properties and formulas for exponential integrals
Real values for real arguments
For real values of 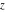 , the values of the gamma function , the values of the gamma function  are real (or infinity). For real values of the parameter are real (or infinity). For real values of the parameter 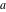 and positive arguments and positive arguments 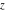 , , 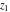 , , 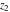 , the values of the gamma functions , the values of the gamma functions 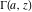 , , 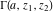 , , 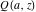 , , 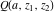 , and , and 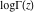 are real (or infinity). are real (or infinity).
Simple values at zero
The gamma functions 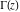 , , 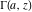 , , 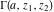 , , 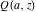 , , 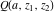 , , 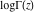 , , 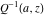 , and , and 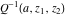 have the following values at zero arguments: have the following values at zero arguments:
Specific values for specialized variables
If the variable 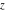 is equal to is equal to 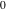 and and 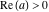 , the incomplete gamma function , the incomplete gamma function 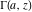 coincides with the gamma function coincides with the gamma function 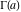 and the corresponding regularized gamma function and the corresponding regularized gamma function 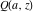 is equal to is equal to 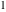 : :
In cases when the parameter  equals equals  , the incomplete gamma functions , the incomplete gamma functions 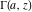 and and 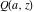 can be expressed as an exponential function multiplied by a polynomial. In cases when the parameter can be expressed as an exponential function multiplied by a polynomial. In cases when the parameter  equals equals 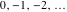 , the incomplete gamma function , the incomplete gamma function 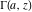 can be expressed with the exponential integral can be expressed with the exponential integral 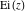 , exponential, and logarithmic functions, but the regularized incomplete gamma function , exponential, and logarithmic functions, but the regularized incomplete gamma function 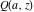 is equal to is equal to 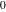 . In cases when the parameter . In cases when the parameter 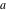 equals equals 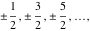 the incomplete gamma functions the incomplete gamma functions 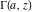 and and 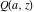 can be expressed through the complementary error function can be expressed through the complementary error function  and the exponential function, for example: and the exponential function, for example:
These formulas are particular cases of the following general formulas:
If the argument 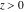 , the log‐gamma function , the log‐gamma function  can be evaluated at these points where the gamma function can be evaluated in closed form. The log‐gamma function can be evaluated at these points where the gamma function can be evaluated in closed form. The log‐gamma function 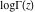 can also be represented recursively in terms of can also be represented recursively in terms of 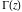 for for 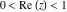 : :
The generalized incomplete gamma functions 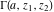 and and  in particular cases can be represented through incomplete gamma functions in particular cases can be represented through incomplete gamma functions 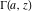 and and 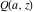 and the gamma function and the gamma function 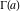 : :
The inverse of the regularized incomplete gamma functions  and and 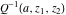 for particular values of arguments satisfy the following relations: for particular values of arguments satisfy the following relations:
Analyticity
The gamma functions 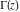 , , 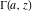 , , 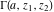 , , 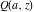 , , 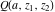 , and , and 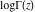 are defined for all complex values of their arguments. are defined for all complex values of their arguments.
The functions 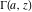 and and 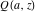 are analytic functions of are analytic functions of 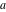 and and 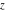 over the whole complex over the whole complex 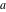 ‐ and ‐ and 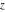 ‐planes excluding the branch cut on the ‐planes excluding the branch cut on the 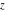 ‐plane. For fixed ‐plane. For fixed  , they are entire functions of , they are entire functions of 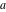 . The functions . The functions  and and 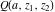 are analytic functions of are analytic functions of 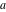 , ,  , and , and 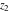 over the whole complex over the whole complex 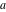 ‐, ‐, 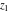 ‐, and ‐, and 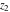 ‐planes excluding the branch cuts on the ‐planes excluding the branch cuts on the  ‐ and ‐ and 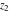 ‐planes. For fixed ‐planes. For fixed 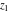 and and 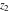 , they are entire functions of , they are entire functions of 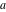 . .
The function  is an analytical function of is an analytical function of 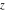 over the whole complex over the whole complex 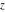 ‐plane excluding the branch cut. ‐plane excluding the branch cut.
Poles and essential singularities
For fixed 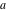 , the functions , the functions 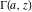 and and 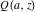 have an essential singularity at have an essential singularity at 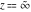 . At the same time, the point . At the same time, the point 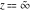 is a branch point for generic is a branch point for generic 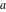 . For fixed . For fixed 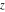 , the functions , the functions 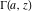 and and 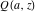 have only one singular point at have only one singular point at 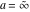 . It is an essential singularity. . It is an essential singularity.
For fixed 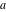 , the functions , the functions 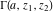 and and 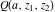 have an essential singularity at have an essential singularity at 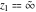 (for fixed (for fixed 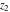 ) and at ) and at 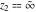 (for fixed (for fixed 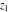 ). At the same time, the points ). At the same time, the points 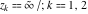 are branch points for generic are branch points for generic  . For fixed . For fixed 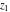 and and 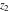 , the functions , the functions  and and 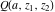 have only one singular point at have only one singular point at 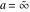 . It is an essential singularity. . It is an essential singularity.
The function 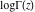 does not have poles or essential singularities. does not have poles or essential singularities.
Branch points and branch cuts
For fixed 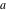 , not a positive integer, the functions , not a positive integer, the functions 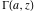 and and 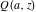 have two branch points: have two branch points: 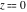 and and 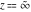 . .
For fixed 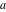 , not a positive integer, the functions , not a positive integer, the functions 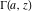 and and  are single‐valued functions on the are single‐valued functions on the 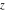 ‐plane cut along the interval ‐plane cut along the interval 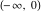 , where they are continuous from above: , where they are continuous from above:
For fixed 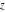 , the functions , the functions 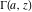 and and  do not have branch points and branch cuts. do not have branch points and branch cuts.
For fixed 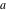 , , 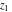 or fixed or fixed  , , 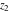 (with (with 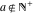 ), the functions ), the functions 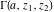 and and 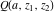 have two branch points with respect to have two branch points with respect to 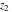 or or 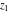 : : 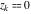 , , 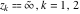 . .
For fixed 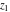 and and  , the functions , the functions 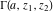 and and 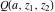 are single‐valued functions on the are single‐valued functions on the 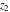 ‐plane cut along the interval ‐plane cut along the interval 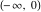 , where they are continuous from above: , where they are continuous from above:
For fixed 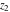 and and 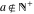 , the functions , the functions 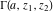 and and 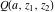 are single‐valued functions on the are single‐valued functions on the  ‐plane cut along the interval ‐plane cut along the interval 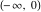 , where they are continuous from above: , where they are continuous from above:
For fixed 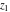 and and  , the functions , the functions 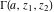 and and 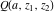 do not have branch points and branch cuts. do not have branch points and branch cuts.
The function 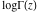 has two branch points: has two branch points: 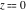 and and 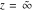 . .
The function 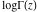 is a single‐valued function on the is a single‐valued function on the 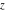 ‐plane cut along the interval ‐plane cut along the interval 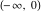 , where it is continuous from above: , where it is continuous from above:
Periodicity
The gamma functions 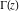 , ,  , , 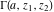 , , 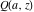 , , 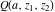 , the log‐gamma function , the log‐gamma function 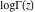 , and their inverses , and their inverses 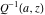 and and  do not have periodicity. do not have periodicity.
Parity and symmetry
The gamma functions 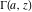 , , 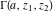 , ,  , , 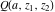 , and the log‐gamma function , and the log‐gamma function 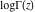 have mirror symmetry (except on the branch cut intervals): have mirror symmetry (except on the branch cut intervals):
Two of the gamma functions have the following permutation symmetry:
Series representations
The gamma functions 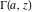 , , 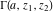 , ,  , ,  , the log‐gamma function , the log‐gamma function 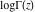 , and the inverse , and the inverse 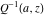 have the following series expansions: have the following series expansions:
Asymptotic series expansions
The asymptotic behavior of the gamma functions 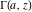 and and 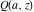 , the log‐gamma function , the log‐gamma function 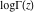 , and the inverse , and the inverse 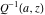 can be described by the following formulas (only the main terms of asymptotic expansion are given): can be described by the following formulas (only the main terms of asymptotic expansion are given):
Integral representations
The gamma functions 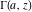 , , 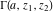 , , 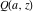 , , 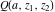 , and the log‐gamma function , and the log‐gamma function  can also be represented through the following integrals: can also be represented through the following integrals:
Transformations
The argument of the log‐gamma function 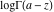 can be simplified if can be simplified if 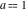 or or  : :
Multiple arguments
The log‐gamma function 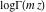 with with 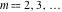 can be represented by a formula that follows from the corresponding multiplication formula for the gamma function can be represented by a formula that follows from the corresponding multiplication formula for the gamma function 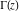 : :
Identities
The gamma functions 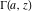 , , 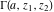 , , 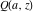 , , 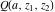 , and the log‐gamma function , and the log‐gamma function 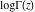 satisfy the following recurrence identities: satisfy the following recurrence identities:
The previous formulas can be generalized to the following recurrence identities with a jump of length n:
Representations of derivatives
The derivatives of the gamma functions 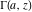 , , 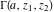 , ,  , and , and 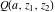 with respect to the variables with respect to the variables 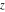 , , 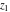 , and , and 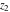 have simple representations in terms of elementary functions: have simple representations in terms of elementary functions:
The derivatives of the log‐gamma function 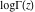 and the inverses of the regularized incomplete gamma functions and the inverses of the regularized incomplete gamma functions  , and , and 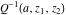 with respect to the variables with respect to the variables 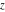 , , 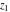 , and , and 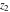 have more complicated representations by the formulas: have more complicated representations by the formulas:
The derivative of the exponential integral 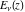 by its parameter by its parameter 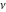 can be represented in terms of the regularized hypergeometric function can be represented in terms of the regularized hypergeometric function 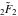 : :
The derivatives of the gamma functions  , ,  , , 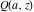 , and , and 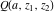 , and their inverses , and their inverses 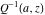 and and 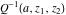 with respect to the parameter with respect to the parameter 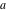 can be represented in terms of the regularized hypergeometric function can be represented in terms of the regularized hypergeometric function 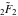 : :
The symbolic 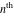 -order derivatives of all gamma functions -order derivatives of all gamma functions 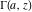 , , 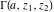 , , 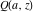 , , 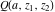 , and their inverses , and their inverses 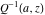 , and , and 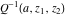 have the following representations: have the following representations:
Differential equations
The gamma functions 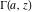 , , 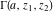 , ,  , and , and 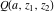 satisfy the following second-order linear differential equations: satisfy the following second-order linear differential equations:
where 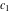 and and 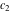 are arbitrary constants. are arbitrary constants.
The log‐gamma function 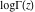 satisfies the following simple first-order linear differential equation: satisfies the following simple first-order linear differential equation:
The inverses of the regularized incomplete gamma functions  and and  satisfy the following ordinary nonlinear second-order differential equation: satisfy the following ordinary nonlinear second-order differential equation:
Applications of gamma functions
The gamma functions are used throughout mathematics, the exact sciences, and engineering. In particular, the incomplete gamma function is used in solid state physics and statistics, and the logarithm of the gamma function is used in discrete mathematics, number theory, and other fields of sciences.
|