|
Almost simultaneously with the development of the mathematical theory of factorials, binomials, and gamma functions in the 18th century, some mathematicians introduced and studied related special functions that are basically derivatives of the gamma function. These functions appeared in coefficients of the series expansions of the solutions in the logarithmic cases of some important differential equations. They appear in the Bessel differential equation for example. So functions in this group are called the differentiated gamma functions.
The harmonic numbers 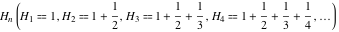 for integer for integer  have a very long history. The famous Pythagoras of Samos (569–475 B.C.) was the first to encounter the harmonic series have a very long history. The famous Pythagoras of Samos (569–475 B.C.) was the first to encounter the harmonic series
in connection with string vibrations and his special interest in music.
Richard Suiseth (14th century) and Nicole d’Oresme (1350) studied the harmonic series and discovered that it diverges. Pietro Mengoli (1647) proved the divergence of the harmonic series. Nicolaus Mercator (1668) studied the harmonic series corresponding to the series of  and Jacob Bernoulli (1689) again proved the divergence of the harmonic series. The harmonic numbers and Jacob Bernoulli (1689) again proved the divergence of the harmonic series. The harmonic numbers 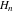 with integer with integer 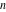 also appeared in an article of G. W. Leibniz (1673). also appeared in an article of G. W. Leibniz (1673).
In his famous work, J. Stirling (1730) not only found the asymptotic formula for factorial 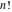 , but used the digamma psi function , but used the digamma psi function 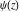 (related to the harmonic numbers), which is equal to the derivative of the logarithm from the gamma function ( (related to the harmonic numbers), which is equal to the derivative of the logarithm from the gamma function (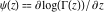 ). Later L. Euler (1740) also used harmonic numbers and introduced the generalized harmonic numbers ). Later L. Euler (1740) also used harmonic numbers and introduced the generalized harmonic numbers  . .
The digamma function 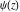 and its derivatives and its derivatives  of positive integer orders of positive integer orders 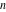 were widely used in the research of A. M. Legendre (1809), S. Poisson (1811), C. F. Gauss (1810), and others. M. A. Stern (1847) proved the convergence of the Stirling series for the digamma function: were widely used in the research of A. M. Legendre (1809), S. Poisson (1811), C. F. Gauss (1810), and others. M. A. Stern (1847) proved the convergence of the Stirling series for the digamma function:
At the end of the 20th century, mathematicians began to investigate extending the function 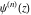 to all complex values of to all complex values of  (B. Ross (1974), N. Grossman (1976)). R. W. Gosper (1997) defined and studied the cases (B. Ross (1974), N. Grossman (1976)). R. W. Gosper (1997) defined and studied the cases 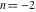 and and 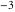 . V. S. Adamchik (1998) suggested the definition . V. S. Adamchik (1998) suggested the definition 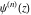 for complex for complex 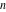 using Liouville's fractional integration operator. A natural extension of using Liouville's fractional integration operator. A natural extension of 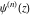 for the complex order for the complex order 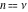 was recently suggested by O. I. Marichev (2001) during the development of subsections with fractional integro‐differentiation for the Wolfram Functions website and the technical computing system Mathematica: was recently suggested by O. I. Marichev (2001) during the development of subsections with fractional integro‐differentiation for the Wolfram Functions website and the technical computing system Mathematica:
|