|
The digamma function 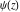 , polygamma function , polygamma function 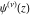 , harmonic number , harmonic number 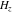 , and generalized harmonic number , and generalized harmonic number 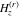 are defined by the following formulas (the first formula is a general definition for complex arguments and the second formula is for positive integer arguments): are defined by the following formulas (the first formula is a general definition for complex arguments and the second formula is for positive integer arguments):
Here 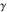 is the Euler gamma constant is the Euler gamma constant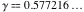 : :
Remark: This formula presents the (not unique) continuation of the classical definition of 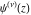 from positive integer values of from positive integer values of 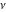 to its arbitrary complex values. to its arbitrary complex values.
For positive integer  and arbitrary complex and arbitrary complex 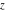 , , 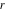 , the following definitions are commonly used: , the following definitions are commonly used:
The previous definition for 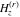 uses the Mathematica definition for the Hurwitz zeta function uses the Mathematica definition for the Hurwitz zeta function 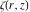 . Branch cuts and related properties are thus inherited from . Branch cuts and related properties are thus inherited from  . .
The previous functions are interconnected and belong to the differentiated gamma functions group. These functions are widely used in the coefficients of series expansions for many mathematical functions (especially the so‐called logarithmic cases).
|