|
General
The probability integral (error function)  has a long history beginning with the articles of A. de Moivre (1718–1733) and P.‐S. Laplace (1774) where it was expressed through the following integral: has a long history beginning with the articles of A. de Moivre (1718–1733) and P.‐S. Laplace (1774) where it was expressed through the following integral:
Later C. Kramp (1799) used this integral for the definition of the complementary error function 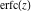 . P.‐S. Laplace (1812) derived an asymptotic expansion of the error function. . P.‐S. Laplace (1812) derived an asymptotic expansion of the error function.
The probability integrals were so named because they are widely applied in the theory of probability, in both normal and limit distributions.
To obtain, say, a normal distributed random variable from a uniformly distributed random variable, the inverse of the error function, namely 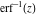 is needed. The inverse was systematically investigated in the second half of the twentieth century, especially by J. R. Philip (1960) and A. J. Strecok (1968). is needed. The inverse was systematically investigated in the second half of the twentieth century, especially by J. R. Philip (1960) and A. J. Strecok (1968).
|