Indefinite integration For the direct function Integration of the derivative gives the original function. The integral of the sum gives the sum of the integrals. The constant factor can be placed outside of the integral. This formula reflects the changing variables rule in the integral. This formula reflects the integration by parts rule. This formula reflects the rule. The integral of the sum is equal to the sum of the integrals of the summands (under some restrictions for convergence of the occurring infinite series). The integral from the power series is equal to the sum of the integrals from each term of the series (inside some circle of convergence). Repeated indefinite integration This formula reflects repeated indefinite integration, where the integration in Mathematica should be performed with the option GenerateConditions->False: Integrate[(z-t)n-1(n-1)!f[t],{t,0,z}, GenerateConditionsFalse]. This formula reflects repeated indefinite integration, where the integration in Mathematica should be performed with the option GenerateConditions->False: Integrate[(Log[z]-Log[t])n-1t(n-1)!f[t],{t,0,z}, GenerateConditionsFalse]. Definite integration For the direct function This formula reflects . This formula reflects . This formula is called Orthogonality See Generalized Fourier series in the section Series representations. Cauchy integrals This formula is called along the piecewise smooth contour 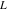 (which can be closed or opened). The (which can be closed or opened). The 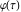 must be continuous along must be continuous along 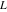 , but it must also meet a more stringent test known as the . The function , but it must also meet a more stringent test known as the . The function 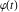 satisfies the Hölder condition if, for two arbitrary points satisfies the Hölder condition if, for two arbitrary points 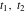 on the curve, on the curve, 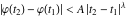 for some positive constants for some positive constants 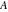 and and  . The Cauchy‐type integral is analytic everywhere on the complex plane except on the contour . The Cauchy‐type integral is analytic everywhere on the complex plane except on the contour 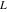 itself, which is a singular line for this integral. Since the integral contains a factor (called the kernel) in the form of itself, which is a singular line for this integral. Since the integral contains a factor (called the kernel) in the form of 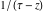 , it diverges at , it diverges at 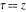 for any for any 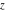 lying on lying on 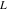 . . This formula is called the for the Cauchy integral. It is valid if 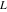 is a closed, smooth contour enclosing the region is a closed, smooth contour enclosing the region  on the complex plane, and the function on the complex plane, and the function 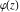 is analytic over is analytic over 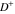 , continuous over , continuous over 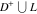 , and , and 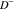 represents the region outside of represents the region outside of 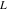 . . Singular integrals In this Cauchy‐type integral, the singular point 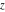 belongs to the contour belongs to the contour 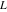 and under the integrand function has a nonintegrable singularity. That is why this improper integral is called a . It can be evaluated, however, if a small neighborhood around this singularity and under the integrand function has a nonintegrable singularity. That is why this improper integral is called a . It can be evaluated, however, if a small neighborhood around this singularity  is removed from the path of integration. The corresponding limit, as the size of the neighborhood shrinks to zero, is the of this divergent integral. For example: is removed from the path of integration. The corresponding limit, as the size of the neighborhood shrinks to zero, is the of this divergent integral. For example: In this example, 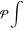 represents the Cauchy principal value, and the contour represents the Cauchy principal value, and the contour  is simply a straight segment on the real axis from is simply a straight segment on the real axis from 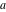 to to 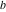 ; in other words, ; in other words, 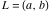 . Rather than integrating from . Rather than integrating from  through the point through the point 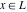 to the point b, you can integrate on the intervals to the point b, you can integrate on the intervals  and and 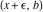 and then add these results to arrive at a value. By taking the limit of this calculation as and then add these results to arrive at a value. By taking the limit of this calculation as 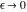 , you can state the principal value. , you can state the principal value. This formula represents the Cauchy principal value of singular curvilinear integrals by the curve 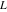 with a circular neighborhood with a circular neighborhood 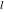 , centered on , centered on 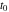 and of radius ϱ, removed. and of radius ϱ, removed. Sokhotskii formulas General This formula represents the function 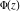 as a piecewise analytic function in the case when as a piecewise analytic function in the case when  is a closed, smooth contour enclosing the region is a closed, smooth contour enclosing the region 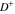 on the complex plane and on the complex plane and 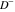 represents the region outside of represents the region outside of 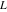 . If . If 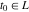 , the values Φ+(t0) and Φ-(t0) can be defined as the following limits: , the values Φ+(t0) and Φ-(t0) can be defined as the following limits: If 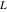 is an open contour with endpoints is an open contour with endpoints 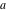 and and 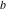 , you can add an additional arbitrary curve segment connecting , you can add an additional arbitrary curve segment connecting  to to 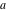 (with the sense that (with the sense that 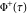 corresponds to the limiting value from the left) and assign corresponds to the limiting value from the left) and assign 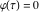 along this new segment. This extension allows you to apply the definitions for along this new segment. This extension allows you to apply the definitions for 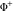 and and 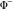 to open contours to open contours  . . These two formulas are called the. They were first derived by Y. V. Sokhotskii in 1873. Because they were later given a more rigorous treatment by J. Plemelj in 1908, they are often referred to as the Plemelj formulas. Sometimes the name Sokhotskii–Plemelj formulas is used. The second of these formulas can be obtained from the Sokhotskii formulas by addition and subtraction. In particular, if 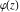 is analytical over is analytical over  , then , then 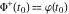 and and 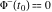 . . If the contour  is a finite or infinite segment of the real axis, is a finite or infinite segment of the real axis, 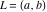 , these formulas hold for all , these formulas hold for all 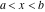 , and so , and so 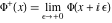 , , 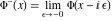 . Thus . Thus  is an analytic function with a jump discontinuity at is an analytic function with a jump discontinuity at 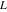 , and the size of the jump is determined by the Sokhotskii formulas. , and the size of the jump is determined by the Sokhotskii formulas. Example: The exponential integral Ei After evaluation of this integral, you get: For arbitrary 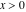 , the Sokhotskii formulas give the following values: , the Sokhotskii formulas give the following values: It is important to note that for 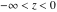 , the function , the function 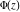 is analytic and its limit values taken from either side of the real axis should agree with each other. This gives the relations: is analytic and its limit values taken from either side of the real axis should agree with each other. This gives the relations: This leads to the following behavior of 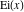 : : Example: Beta-type integral This integral can be called a beta‐type integral. It can be evaluated by the following formulas: For arbitrary 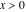 , the Sokhotskii formulas give the following results when you take into account the fact that, as , the Sokhotskii formulas give the following results when you take into account the fact that, as 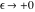 , , 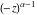 is continuous for is continuous for 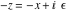 but has a jump of size but has a jump of size 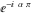 compared to when it is approached from the other side, compared to when it is approached from the other side, 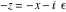 . . |