Exponential Fourier transform Definition This formula is the definition of the exponential Fourier transform of the function 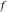 with respect to the variable with respect to the variable 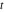 . If the integral does not converge, the value of . If the integral does not converge, the value of 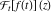 is defined in the sense of generalized functions for functions is defined in the sense of generalized functions for functions 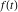 that do not grow faster than polynomials at that do not grow faster than polynomials at 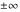 . . Properties Linearity This formula reflects the linearity of the exponential Fourier transform. Reflection This formula is called the reflection property of the exponential Fourier transform. Dilation This formula reflects the scaling or dilation property of the exponential Fourier transform. Shifting or translation This formula reflects the shifting or translation property of the exponential Fourier transform. Modulation This formula reflects the modulation property of the exponential Fourier transform. This formula reflects the modulation property of the exponential Fourier transform. This formula reflects the modulation property of the exponential Fourier transform. Power scaling The power scaling property shows that multiplication of a function by 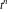 corresponds to the corresponds to the  derivative of the exponential Fourier transform. derivative of the exponential Fourier transform. This formula shows that multiplication of a function by 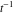 corresponds to integration of the exponential Fourier transform. corresponds to integration of the exponential Fourier transform. Multiplication The multiplication property shows that the exponential Fourier transform of a product gives the convolution of the exponential Fourier transform divided by 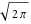 . . Conjugation This formula reflects the conjugation property of the exponential Fourier transform. Derivative The derivative property shows that the exponential Fourier transform of the 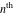 derivative gives the product of the power function on the exponential Fourier transform. derivative gives the product of the power function on the exponential Fourier transform. Integral This formula shows that the exponential Fourier transform of an integral gives the product of the power function and the exponential Fourier transform plus an expression that includes a Dirac delta function. Parseval identity This formula is called the Parseval identity. This Bessel’s equality follows from the Parseval identity, when 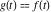 . . Convolution theorem This Fourier convolution theorem or convolution (Faltung) theorem for the exponential Fourier transform shows that the Fourier transform of a convolution is equal to the product of the Fourier transform multiplied by 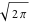 . . Relations with other integral transforms With inverse exponential Fourier transform This formula reflects the relation between direct and inverse exponential Fourier transforms. In the point 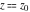 , where , where 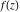 has a jump discontinuity the composition of the inverse and direct exponential Fourier transforms converges to the mean has a jump discontinuity the composition of the inverse and direct exponential Fourier transforms converges to the mean 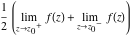 . . With Fourier cosine and sine transforms This formula shows how the exponential Fourier transform can be represented through cosine and sine Fourier transforms from even and odd parts. With Laplace transform This formula shows how the exponential Fourier transform can be represented through the Laplace transform. With Mellin transform This formula shows how the exponential Fourier transform can be represented through the Mellin transform. With Z-transform This formula shows how the exponential Fourier transform can be represented through the Z‐transform. Inverse exponential Fourier transform Definition This formula is the definition of the inverse exponential Fourier transform of the function 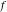 with respect to the variable with respect to the variable 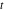 . If the integral does not converge, the value of . If the integral does not converge, the value of 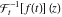 is defined in the sense of generalized functions. is defined in the sense of generalized functions. Relations with other integral transforms With exponential Fourier transform This near‐equivalence identity shows that the inverse exponential Fourier transform in the point 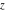 coincides with the direct Fourier transform in the point coincides with the direct Fourier transform in the point 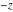 . . This near‐equivalence identity shows that the inverse exponential Fourier transform in the point  coincides with the direct Fourier transform in the point coincides with the direct Fourier transform in the point 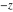 . . This formula reflects the relation between the direct and inverse exponential Fourier transforms. In the point 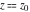 , where , where 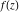 has a jump discontinuity, the composition of inverse and direct exponential Fourier transforms converges to the mean has a jump discontinuity, the composition of inverse and direct exponential Fourier transforms converges to the mean 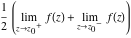 . . Multiple exponential Fourier transform Definition This formula is the definition of the double exponential Fourier transform of the function 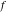 with respect to the variables with respect to the variables  , , 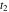 . If the integral does not converge, the value of . If the integral does not converge, the value of  is defined in the sense of generalized functions. is defined in the sense of generalized functions. This formula is the definition of the multiple exponential Fourier transform of the function 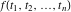 with respect to the variables with respect to the variables 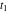 , , 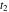 ,…, ,…, 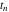 over over 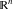 . If this integral does not converge, the value of . If this integral does not converge, the value of 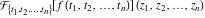 is defined in the sense of generalized functions. is defined in the sense of generalized functions. Inverse multiple exponential Fourier transform Definition This formula is the definition of the inverse double exponential Fourier transform of the function  with respect to the variables with respect to the variables  , , 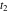 . If this integral does not converge, the value of . If this integral does not converge, the value of  is defined in the sense of generalized functions. is defined in the sense of generalized functions. This formula is the definition of the inverse multiple exponential Fourier transform of the function 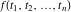 with respect to the variables with respect to the variables 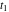 , , 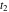 ,…, ,…,  over over 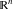 . If this integral does not converge, the value of . If this integral does not converge, the value of  is defined in the sense of generalized functions. is defined in the sense of generalized functions. Relations with other integral transforms With multiple exponential Fourier transform This near‐equivalence identity shows that the inverse multiple exponential Fourier transform in the point 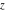 coincides with the direct multiple exponential Fourier transform at the point coincides with the direct multiple exponential Fourier transform at the point 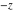 . . Fourier transform (continuous -> discrete) Definition General properties Linearity Reflection Dilation Shifting or translation Modulation Multiplication Conjugation Derivative Grouping Summation Parseval identity Convolution theorem Relations with other integral transforms With inverse Fourier transform (continuous -> discrete) Inverse Fourier transform (continuous -> discrete) Definition Relations with other integral transforms With Fourier transform (continuous -> discrete) Fourier transform (discrete -> continuous) Definition General properties Linearity Reflection Dilation Shifting or translation Modulation Power scaling Multiplication Conjugation Sampling Zero packing Parseval identity Convolution theorem Relations with other integral transforms With inverse Fourier transform (discrete -> continuous) Inverse Fourier transform (discrete -> continuous) Definition Relations with other integral transforms With Fourier transform (discrete -> continuous) Fourier transform (discrete -> discrete) Definition General properties Linearity Reflection Dilation Shifting or translation Modulation Multiplication Conjugation Repeat Zero packing Summation Parseval identity Convolution theorem Relations with other integral transforms With inverse Fourier transform (discrete -> discrete) Inverse Fourier transform (discrete -> discrete) Definition Relations with other integral transforms With Fourier transform (discrete -> discrete) Fourier cosine transform Definition This formula is the definition of the Fourier cosine transform of the function  with respect to the variable with respect to the variable 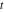 . If the integral does not converge, the value of . If the integral does not converge, the value of 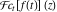 is defined in the sense of generalized functions. is defined in the sense of generalized functions. General properties Linearity This formula reflects the linearity of the Fourier cosine transform. Scaling This formula reflects the scaling property of the Fourier cosine transform. Modulation This formula reflects the modulation property of the Fourier cosine transform. This formula reflects the modulation property of the Fourier cosine transform. Parity This formula shows how the Fourier cosine transform can be applied to the difference between the even part of 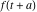 and the odd part of and the odd part of 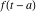 . . This formula shows how the Fourier cosine transform can be applied to the sum of the even part of 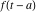 and the odd part of and the odd part of 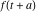 . . Power scaling This formula shows that multiplication of a function by 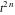 corresponds to the corresponds to the  derivative of the Fourier cosine transform. derivative of the Fourier cosine transform. This formula shows that multiplication of a function by  corresponds to the corresponds to the 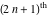 derivative of the Fourier sine transform. derivative of the Fourier sine transform. Derivative This formula shows that the Fourier cosine transform of an even-order derivative gives the product of the power function with the Fourier cosine transform plus some even polynomial. This formula shows that the Fourier cosine transform of an odd-order derivative gives the product of a power function with the Fourier sine transform plus some even polynomial. Convolution related This formula shows that the Fourier cosine transform of a convolution gives the product of Fourier cosine transforms multiplied by 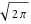 . . Integral This formula shows that the Fourier cosine transform of an indefinite integral with a variable lower limit gives the product of the Fourier sine transforms by 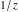 . . Limit at infinity This Riemann–Lebesgue theorem shows that the Fourier cosine transform 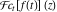 converges to zero as converges to zero as 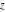 tends to infinity for some classes of the function tends to infinity for some classes of the function 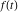 . . Relations with other integral transforms With inverse Fourier cosine transform This formula reflects the relation between the direct and the inverse Fourier cosine transforms. In the point 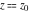 , where , where 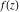 has a jump discontinuity, the composition of the inverse and the direct Fourier cosine transforms converges to the mean has a jump discontinuity, the composition of the inverse and the direct Fourier cosine transforms converges to the mean 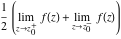 . . With exponential Fourier transform This formula reflects the relation between the direct and the inverse exponential Fourier transforms. With Laplace transform This formula represents the Fourier cosine transform through Laplace transforms. Inverse Fourier cosine transform Definition This formula is the definition of the inverse Fourier cosine transform of the function 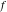 with respect to the variable with respect to the variable 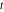 . If the integral does not converge, the value of . If the integral does not converge, the value of 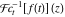 is defined in the sense of generalized functions. is defined in the sense of generalized functions. Relations with other integral transforms With Fourier cosine transform This formula shows that the inverse Fourier cosine transform coincides with the direct Fourier cosine transform. Fourier sine transform Definition This formula is the definition of the Fourier sine transform of the function 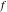 with respect to the variable with respect to the variable  . If the integral does not converge, the value of . If the integral does not converge, the value of 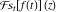 is defined in the sense of generalized functions. is defined in the sense of generalized functions. General properties Linearity This formula reflects the linearity of the Fourier sine transform. Scaling This formula reflects the scaling property of the Fourier sine transform. Modulation This formula reflects the modulation property of the Fourier sine transform. This formula reflects the modulation property of the Fourier sine transform. Parity This formula shows how the Fourier sine transform can be applied to the difference between the even part of 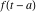 and the odd part of and the odd part of 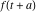 . . This formula shows how the Fourier sine transform can be applied to a sum of the even part of 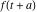 and the odd part of and the odd part of 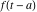 . . Power scaling This formula shows that multiplication of a function by 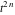 corresponds to the corresponds to the  derivative of the Fourier sine transform. derivative of the Fourier sine transform. This formula shows that multiplication of a function by 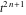 corresponds to the corresponds to the  derivative of the Fourier cosine transform. derivative of the Fourier cosine transform. Derivative This formula shows that the Fourier sine transform of an even-order derivative gives the product of the power function and the Fourier sine transform plus some odd‐order polynomial. This formula shows that the Fourier sine transform of an odd-order derivative gives the product of the power function and the Fourier cosine transform plus some odd‐order polynomial. Convolution related This formula shows that the Fourier sine transform of a convolution gives the product of the Fourier sine and the Fourier cosine transforms multiplied by 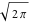 . . Integral This formula shows that the Fourier sine transform of an indefinite integral with a variable lower limit gives the difference of the Fourier cosine transforms in 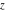 and and 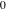 multiplied by multiplied by 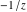 . . Limit at infinity The Riemann–Lebesgue theorem shows that the Fourier sine transform 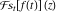 converges to zero as converges to zero as  tends to infinity for some classes of function tends to infinity for some classes of function 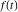 . . Relations with other integral transforms With inverse Fourier sine transform This formula reflects the relation between the direct and the inverse Fourier sine transforms. At the point  , where , where 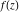 has a jump discontinuity, the composition of the inverse and the direct Fourier sine transforms converges to the mean has a jump discontinuity, the composition of the inverse and the direct Fourier sine transforms converges to the mean 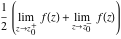 . . With exponential Fourier transform This formula represents the Fourier sine transform through the exponential Fourier transform. With Laplace transform This formula represents the Fourier sine transform through the Laplace transforms. Inverse Fourier sine transform Definition This formula is the definition of the inverse Fourier sine transform of the function  with respect to the variable with respect to the variable 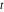 . If the integral does not converge, the value of . If the integral does not converge, the value of 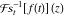 is defined in the sense of generalized functions. is defined in the sense of generalized functions. Relations with other integral transforms With Fourier sine transform This formula shows that the inverse Fourier sine transform coincides with the direct Fourier sine transform. Laplace transform Definition This formula is the definition of the Laplace transform of the function 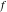 with respect to the variable with respect to the variable 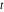 . If the integral does not converge, the value of . If the integral does not converge, the value of 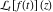 is defined in the sense of generalized functions. is defined in the sense of generalized functions. General properties Linearity This formula reflects the linearity of the Laplace transform. Shift This shift theorem shows that the Laplace transform of a product with an exponential function gives the Laplace transform in the shifted point. Power scaling This formula shows that differentiation of a Laplace transform corresponds to multiplication of the original function by 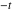 . . This formula shows that differentiation of a Laplace transform of order 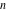 corresponds to multiplication of the original function by corresponds to multiplication of the original function by 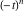 . . Product This formula represents the Laplace transform of a product  and and 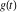 through the contour integral along a vertical line from the corresponding product of Laplace transforms. through the contour integral along a vertical line from the corresponding product of Laplace transforms. Derivative This time differentiation relation gives the representation for the Laplace transform of the first derivative. This time differentiation relation gives the representation of the Laplace transform of the 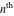 derivative. derivative. Integral This formula shows that the Laplace transform of an indefinite integral gives the product of the reciprocal function of 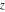 by the Laplace transform of the function. by the Laplace transform of the function. This formula shows that the Laplace transform of the repeated indefinite integral 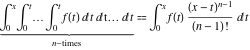 gives the product of the power function gives the product of the power function 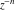 on Laplace transform. on Laplace transform. Convolution The convolution theorem or convolution (Faltung) theorem for the Laplace transform shows that the Laplace transform of a convolution is equal to the product of Laplace transforms of the convoluted functions. Limit at infinity The initial value theorem shows that limit at infinity of the Laplace transform multiplied by 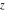 is the one‐sided limit of the initial function at zero. is the one‐sided limit of the initial function at zero. Limit at zero The final value theorem shows that the limit at zero of the Laplace transform multiplied by 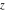 is the limit of the initial function at infinity. is the limit of the initial function at infinity. Sum Relations with other integral transforms With inverse Laplace transform This formula reflects the relation between the direct and the inverse Laplace transforms. This formula reflects the relation between the direct and the inverse Laplace transforms. With exponential Fourier transform This formula shows how the Laplace transform can be represented through the exponential Fourier transform. With Mellin transform This formula shows how the Laplace transform can be represented through the Mellin transform. With Z-transform This formula shows how the Laplace transform can be represented through the Z‐transform. Inverse Laplace transform Definition This formula is the definition of the inverse Laplace integral transform of the function 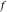 with respect to the variable with respect to the variable  . . This formula is the definition of the inverse Laplace integral transform of the function 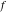 with respect to the variable with respect to the variable 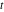 . . This formula is the Post–Widder form of the inverse Laplace integral transform of the function 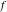 with respect to the variable with respect to the variable 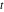 . . Multiple Laplace transform Definition This formula is the definition of the double Laplace transform of the function 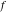 with respect to the variables with respect to the variables 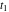 , ,  . . This formula is the definition of multiple Laplace transforms of the function  with respect to the variables with respect to the variables 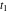 , , 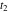 ,…, ,…, 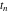 over over 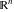 . . Mellin transform Definition This formula is the definition of the Mellin transform of the function 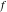 with respect to the variable with respect to the variable 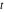 . If the integral does not converge, the value of . If the integral does not converge, the value of  is defined in the sense of generalized functions. Usually, the integral converges in the strip is defined in the sense of generalized functions. Usually, the integral converges in the strip  , where , where 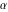 and and 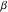 depend on the function depend on the function 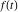 and can assume the values and can assume the values  . For example, . For example, 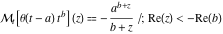 . . General properties Linearity This formula reflects the linearity of the Mellin transform. Scaling The operation reflects the scaling of the original variable 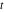 by a positive number by a positive number 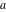 in a Mellin transform. in a Mellin transform. Power This formula reflects the Mellin transform of the function 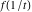 . . The operation provides the Mellin transform of the original variable 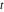 raised to a real power raised to a real power 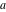 . . Shifting The shift theorem gives the Mellin transform of a product of the original function by some power of 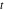 . . The operation gives the Mellin transform of a product of the original function by a power of 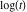 . . Derivative This formula shows that the Mellin transform of an 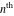 derivative gives the product of a polynomial and the Mellin transform of the function. derivative gives the product of a polynomial and the Mellin transform of the function. This formula shows that the Mellin transform of 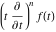 gives the product of a power function and the Mellin transform. gives the product of a power function and the Mellin transform. This formula shows that the Mellin transform of 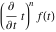 gives the product of the power function and the Mellin transform. gives the product of the power function and the Mellin transform. This formula shows that the Mellin transform of 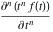 gives the product of a polynomial and the Mellin transform. gives the product of a polynomial and the Mellin transform. This formula shows that the Mellin transform of 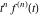 gives the product of a polynomial and the Mellin transform. gives the product of a polynomial and the Mellin transform. Integral This formula shows that the Mellin transform of an indefinite integral gives the product of  and the Mellin transform in the shifted point. and the Mellin transform in the shifted point. This formula shows how the Mellin transform of a repeated indefinite integral gives the product of a rational function and the Mellin transform in the shifted point. This formula shows that the Mellin transform of the indefinite integral with a variable lower limit gives the product of 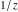 and the Mellin transform in the shift point. and the Mellin transform in the shift point. This formula demonstrates how the Mellin transform of a repeated indefinite integral with variable lower limits gives the product of a rational function amd the Mellin transform in the shifted point. Convolution The Mellin convolution theorem shows that the Mellin transform of a Mellin convolution equals the product of the Mellin transforms. The generalized Mellin convolution theorem shows that the Mellin transform of the generalized Mellin convolution is equal to the product of the Mellin transforms. Parseval This formula is called Mellin–Parseval’s formula. This formula is called Parseval’s formula. This representation can be used for evaluation of the general class of integrals from products of Meijer G functions. Relations with other integral transforms With inverse Mellin transform This formula reflects the relation between the direct and the inverse Mellin transforms. The following theorem holds: if an analytical function 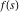 satisfies the restriction satisfies the restriction 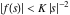 in the strip in the strip 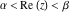 with some constant with some constant 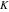 , then the integral , then the integral 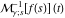 is a continuous function of the variable is a continuous function of the variable 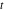 and is its Mellin transform in this strip. and is its Mellin transform in this strip. With exponential Fourier transform This formula shows how the Mellin transform can be represented through the exponential Fourier transform. With Fourier cosine and sine transforms This formula shows how the Mellin transform can be represented through the cosine and the sine Fourier transforms from the even and odd parts of the function. With Mellin transform This formula shows how the Laplace transform can be represented through the Mellin transform. Inverse Mellin transform Definition This formula is the definition of the inverse Mellin integral transform of the function 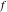 with respect to the variable with respect to the variable 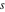 . If the integral does not converge, the value of . If the integral does not converge, the value of 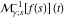 is defined in the sense of generalized functions. The condition on is defined in the sense of generalized functions. The condition on 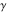 usually has the following form: usually has the following form: 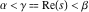 , which represents a vertical strip of convergence for the integral. , which represents a vertical strip of convergence for the integral. Changing the vertical strip of integration 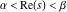 leads to a change in the original function leads to a change in the original function  . For example, in the case of gamma function . For example, in the case of gamma function 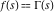 you have you have 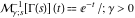 and and 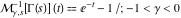 . . Multiple Mellin transform Definition This formula is the definition of the double Mellin transform of the function 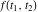 with respect to the variables with respect to the variables  , ,  . . This formula is the definition of the multiple Mellin transform of the function  with respect to the variables with respect to the variables 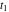 , ,  ,…, ,…, 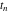 . . General properties Convolution The generalized Mellin convolution theorem shows that the double Mellin transform of a Mellin generalized convolution equals the product of the Mellin transforms in the corresponding points. The generalized Mellin convolution theorem shows that the multiple Mellin transform of a Mellin generalized convolution equals the product of the Mellin transforms in the corresponding points. Hankel transform Definition This formula is the definition of the Hankel integral transform of the function 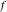 with respect to the variable with respect to the variable 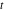 . If this integral does not converge, the value of . If this integral does not converge, the value of 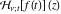 is defined in the sense of generalized functions. is defined in the sense of generalized functions. General properties This formula shows that the inverse Hankel integral transform coincides with the direct Hankel integral transform under the restriction 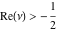 . . Hilbert transform Definition This formula is the definition of the Hilbert transform of the function 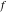 with respect to the variable with respect to the variable 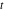 for real for real  . . Inverse Hilbert transform Definition This formula is the definition of the inverse Hilbert transform of the function 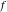 with respect to the variable with respect to the variable 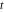 for real for real 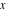 . It coincides with the direct Hilbert transform multiplied by -1. . It coincides with the direct Hilbert transform multiplied by -1. Relations with other integral transforms With Hilbert transform Z-transform Definition This formula is the definition of the Z‐transform of the function 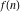 with respect to the discrete variable with respect to the discrete variable 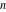 at the complex point at the complex point 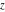 . . General properties Linearity This formula reflects the linearity of the Z‐transform. Shifting This formula reflects the shifting property of the Z‐transform. This formula reflects the shifting property of the Z‐transform. This formula reflects the shifting property of the Z‐transform. Scaling This formula reflects the scaling property of the Z‐transform. This formula shows that multiplication of a function 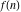 by by 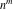 leads to repeated differentiation of the Z‐transform. leads to repeated differentiation of the Z‐transform. This formula shows that multiplication of a function 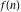 by by 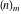 gives the product of gives the product of  and the and the 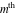 derivative of the Z‐transform. derivative of the Z‐transform. Product The Z‐transform of a product of 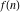 and and 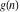 is represented through a contour integral along a simple circle‐type contour is represented through a contour integral along a simple circle‐type contour 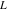 encircling the origin encircling the origin  counterclockwise. All the singular points of the function counterclockwise. All the singular points of the function  are located inside the contour. All the singular points of the function are located inside the contour. All the singular points of the function 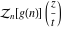 are located outside the contour. are located outside the contour. Parseval The follows from the previous relation for  . The integration is performed along a simple circle‐type contour . The integration is performed along a simple circle‐type contour  encircling the origin encircling the origin  counterclockwise. All the singular points of the function counterclockwise. All the singular points of the function 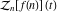 are located inside the contour. All the singular points of the function are located inside the contour. All the singular points of the function 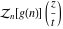 are located outside the contour. are located outside the contour. Correlation The property is called the cross correlation property of the Z‐transform. Convolution The convolution theorem for the Z‐transform shows that the Z‐transform of a convolution sum is equal to the product of the corresponding Z‐transforms. Limit at infinity The analog of the Riemann‐Lebesgue theorem shows that the Z‐transform  at infinity tends to the initial value at infinity tends to the initial value 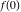 . . This formula shows that the Z‐transform 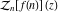 at infinity behaves as at infinity behaves as 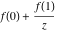 . . Limit at one This formula shows that the expression  near point near point 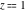 behaves as behaves as 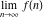 . . Derivative by parameter This formula reflects the differentiation by parameter property of the Z‐transform. Limit by parameter This formula reflects the evaluation limit by parameter property of the Z‐transform. Integration by parameter This formula reflects the integration by parameter property of the Z‐transform. Relations with other integral transforms With inverse Z-transforms This formula reflects the relation between the direct and the inverse Z‐transforms. Inverse Z-transform Definition This formula is the definition of the inverse Z‐transform of the function 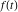 with respect to the variable with respect to the variable  at the discrete point at the discrete point  . The contour integral is performed along a simple circle‐type contour . The contour integral is performed along a simple circle‐type contour 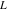 encircling the origin encircling the origin 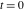 counterclockwise. counterclockwise. Weber transform Definition This formula is the definition of the Weber integral transform of the function  with respect to the variable with respect to the variable 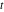 . . Relations with other integral transforms With inverse Weber transform The formula shows that the composition of the direct and the inverse Weber integral transforms gives the original function in a point of continuity. Inverse Weber transform Definition This formula gives the formula for the inverse Weber integral transform. |