Limit operation This formula reflects the definition of a limiting value 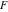 for a function for a function 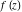 at the point at the point 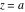 , when , when 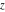 approaches approaches 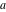 in any direction (the so-called epsilon‐delta definition): the formula in any direction (the so-called epsilon‐delta definition): the formula 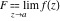 means that the function means that the function 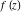 has a limit value has a limit value 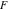 if and only if for all if and only if for all 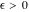 , there exists , there exists 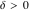 such that such that 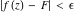 whenever whenever 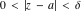 . A limiting value . A limiting value 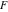 does not always exist, and (if it exists) it does not always coincide with the value of the function at the point does not always exist, and (if it exists) it does not always coincide with the value of the function at the point  (the last value also may not exist). But in the "best situation", when all the values exist and coincide: (the last value also may not exist). But in the "best situation", when all the values exist and coincide: 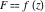 , and the function , and the function 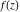 is called continuous at the point is called continuous at the point 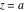 . .  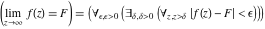 |
This formula reflects the definition of a limiting value 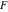 for a function for a function 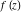 at the infinite point at the infinite point 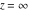 : the formula : the formula 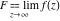 means that the function means that the function 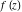 has a limit value has a limit value  if and only if for all if and only if for all  , there exists , there exists  such that such that 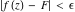 whenever whenever 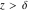 . A limiting value . A limiting value  may not always exist, and (if it exists) may not always coincide with the value of the function at the point may not always exist, and (if it exists) may not always coincide with the value of the function at the point  (the last value also may not exist). But in the "best situation", when all the values exist and coincide: (the last value also may not exist). But in the "best situation", when all the values exist and coincide: 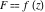 , and the function , and the function  is called continuous at the point is called continuous at the point 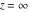 . . This limit shows that analytic functions are continuous functions. This limit defines the derivative of function  at the point at the point 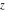 , if it exists. For analytic functions this limit exists. , if it exists. For analytic functions this limit exists. This limit defines the 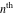 derivative of a function derivative of a function 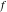 with an argument with an argument 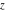 . . L’Hospital’s rule appeared in the first textbook on differential calculus, Treatise of L’Hospital, in 1696. It allows you to evaluate the limit of the ratio of two functions 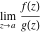 through the limit of the ratio of their derivatives through the limit of the ratio of their derivatives 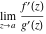 in the cases when in the cases when 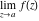 and and  are equal to zero or are equal to zero or 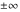 . . This formula reflects the definition of the convergent integral 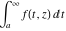 at the argument at the argument 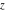 . . This formula reflects the commutativity of the two operations definite integration and limit. This formula reflects the reordering of the two operations infinite summation and limit. This formula reflects the reordering of the two operations infinite product and limit. The Riemann–Lebesgue lemma shows that sine coefficients of the trigonometric Fourier series tend to zero as 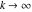 . . The Riemann–Lebesgue lemma shows that cosine coefficients of the trigonometric Fourier series tend to zero as 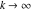 . . |