With inverse function This property is the definition of the inverse function 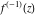 and can hold without additional restrictions on and can hold without additional restrictions on 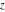 (like (like  , where , where 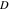 is not is not 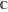 ) for many named functions. In these situations, ) for many named functions. In these situations, 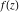 is in most cases free of branch cuts. For example, is in most cases free of branch cuts. For example, 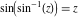 ; here ; here 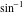 means means 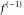 with with 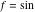 , that is, the inverse sine function (do not confuse this with the reciprocal function , that is, the inverse sine function (do not confuse this with the reciprocal function 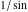 ). ). Some of the functions  are invertible: their inversions are invertible: their inversions 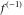 can coincide with the original can coincide with the original 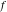 , but for other values of the parameters. For example, the inverse function for the power function , but for other values of the parameters. For example, the inverse function for the power function  is also the power function is also the power function 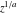 , and the relation , and the relation 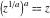 takes place only under the restriction takes place only under the restriction 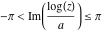 . In general cases the following relation takes place: . In general cases the following relation takes place: 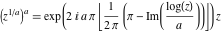 . . The last property for the inverse function of the direct function can be valid under special restrictions for 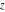 (where typically (where typically 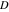 is not is not 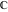 ). For example, ). For example, 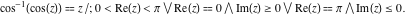 |