Domain and analyticity In the majority of cases, 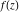 is an analytical function of is an analytical function of 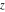 , which is defined in the whole complex , which is defined in the whole complex 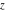 plane (if special restrictions are not shown). plane (if special restrictions are not shown). Symmetries and periodicities This formula is the condition for a function to be even. For example, the function 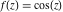 is an even function. is an even function. This formula is the condition for a function to be odd. For example, the function 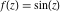 is an odd function. is an odd function. This formula reflects periodicity of function 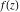 (if (if 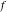 is periodic with period is periodic with period 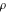 ). The analytic function ). The analytic function 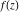 is called periodic if there exists a complex constant is called periodic if there exists a complex constant 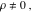 such that such that 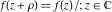 . The number . The number 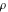 (with minimal value (with minimal value 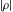 ) is called the period of the function ) is called the period of the function 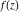 . For example, the functions . For example, the functions 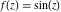 and and 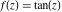 have periods have periods 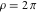 and and 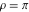 accordingly. accordingly. |