General remarks There are three main possibilities to represent an arbitrary function  as an infinite sum of simple functions. The first is the power series expansion and its two important generalizations, the Laurent series and the Puiseux series. The second is the as an infinite sum of simple functions. The first is the power series expansion and its two important generalizations, the Laurent series and the Puiseux series. The second is the 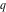 ‐series and Dirichlet series (general and periodic), and the third is the Fourier series (exponential, trigonometric, and generalized Fourier series by the orthogonal systems). These representations provide very general convenient methods for studying a wide range of functions. ‐series and Dirichlet series (general and periodic), and the third is the Fourier series (exponential, trigonometric, and generalized Fourier series by the orthogonal systems). These representations provide very general convenient methods for studying a wide range of functions. The terms of a power series expansion or its generalizations include power functions in the form 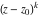 or or 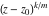 ; the terms in the ; the terms in the 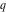 ‐series include expressions like ‐series include expressions like 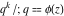 ; the terms in a Dirichlet series include exponential functions in the form ; the terms in a Dirichlet series include exponential functions in the form 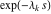 . The Fourier trigonometric series usually provide expansions in terms of . The Fourier trigonometric series usually provide expansions in terms of 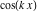 and and 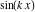 (for trigonometric series) and in terms of (for trigonometric series) and in terms of  (for exponential series). Generalized Fourier series provide expansions in terms of other orthogonal systems of functions, such as the classical orthogonal polynomials. With each of these methods, you can express in closed form an enormous number of non-elementary functions in terms of only simple elementary functions. (for exponential series). Generalized Fourier series provide expansions in terms of other orthogonal systems of functions, such as the classical orthogonal polynomials. With each of these methods, you can express in closed form an enormous number of non-elementary functions in terms of only simple elementary functions. Generalized power series Expansions at z==z0 For the function itself The , first investigated by B. Taylor in 1715, gives the above Taylor expansion for an arbitrary function  at a finite point at a finite point 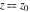 . . The sign ↔ means that the Taylor series should not be taken as purely equal to 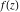 , since it may not converge everywhere on the complex plane. The series converges absolutely in some disk of radius , since it may not converge everywhere on the complex plane. The series converges absolutely in some disk of radius 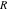 centered on centered on 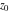 , where , where 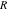 is called the radius of convergence. On the disk is called the radius of convergence. On the disk 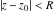 , you can exchange the sign ↔ for ⩵. You can state for most functions that , you can exchange the sign ↔ for ⩵. You can state for most functions that 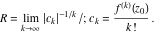 The Taylor series coefficients The Taylor series coefficients  can also be evaluated by the Cauchy integral formula can also be evaluated by the Cauchy integral formula 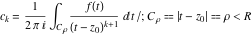 . . There are then three cases for  : either : either  is infinite, is infinite, 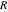 is zero, or is zero, or  is some finite positive number greater than 0. is some finite positive number greater than 0. If 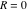 , this series converges only at the point , this series converges only at the point 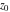 , and the Taylor series offers little analytical benefit. For example, the series , and the Taylor series offers little analytical benefit. For example, the series 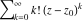 has no disk of convergence around has no disk of convergence around 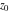 , since the coefficient , since the coefficient 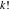 makes the terms grow infinitely large no matter how small makes the terms grow infinitely large no matter how small 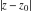 becomes. becomes. If 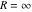 , the series converges in the entire plane. In such cases it either represents an entire transcendental function—as, for example, the series , the series converges in the entire plane. In such cases it either represents an entire transcendental function—as, for example, the series 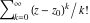 does for the exponential function does for the exponential function 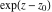 —or it contains only a finite number of terms and therefore represents a polynomial. —or it contains only a finite number of terms and therefore represents a polynomial. If 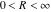 , the sum of the series defines a regular analytic function having at least one singular point on the circle , the sum of the series defines a regular analytic function having at least one singular point on the circle 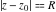 . There may be finitely or infinitely many singular points on the circle, but there must be at least one. The power series . There may be finitely or infinitely many singular points on the circle, but there must be at least one. The power series 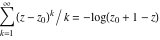 , for example, has only one singular point, at , for example, has only one singular point, at 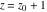 . Other power series have dense sets of singular points on the circle, such as the series . Other power series have dense sets of singular points on the circle, such as the series 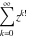 , which has many singular points on the unit circle, the edge of its natural region of analyticity. The same holds true, with the same region of analyticity, for the series representation of the logarithm of InverseEllipticNomeQ: , which has many singular points on the unit circle, the edge of its natural region of analyticity. The same holds true, with the same region of analyticity, for the series representation of the logarithm of InverseEllipticNomeQ: 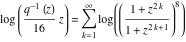 . . Inside the region of convergence of the series, you can exchange the sign ↔ for ⩵ in the preceding Taylor expansion for an arbitrary function  at a finite point at a finite point 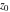 : : Infinite Taylor series expansion can be approximated by the truncated version, the finite Taylor polynomial expansions. But in these cases, instead of the equality sign ⩵, you will use the sign ∝ and an ellipsis … or an explicit Landau O term, for example: The Landau O term 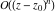 in the preceding relation means that the next expression is bounded near point in the preceding relation means that the next expression is bounded near point 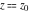 : : For compositions with elementary functions Including power functions Including logarithmic and power functions Expansions at z==0 For the function itself Laurent series The , first studied by P. Laurent in 1843, gives the Laurent expansion for the function  around a finite point around a finite point 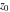 , where , where 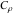 is the circle is the circle 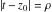 with radius with radius 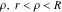 . Here . Here 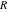 is the radius of convergence of its regular part is the radius of convergence of its regular part 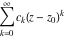 and and  is the radius of convergence of its principal part is the radius of convergence of its principal part  . The coefficient . The coefficient 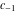 of the power of the power 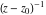 in the Laurent expansion of function in the Laurent expansion of function 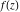 is called the residue of is called the residue of  at the point at the point 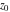 : : If 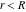 , then the Laurent series converges absolutely in the ring , then the Laurent series converges absolutely in the ring  , where its sum defines an analytic function. If , where its sum defines an analytic function. If 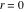 and the principal part includes only a finite number of terms (that is, if and the principal part includes only a finite number of terms (that is, if 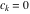 for for  for some for some 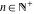 ), then ), then 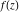 has a pole of order has a pole of order 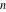 at the point at the point 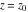 . . For example, the function 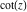 has a pole of order 1 (also called a simple pole) at the point has a pole of order 1 (also called a simple pole) at the point 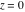 , since it has only one term in the principal part of its Laurent series expansion: , since it has only one term in the principal part of its Laurent series expansion: If 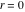 and the principal part includes an infinite number of terms, this analytic function has an essential singularity at the point and the principal part includes an infinite number of terms, this analytic function has an essential singularity at the point 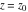 . For example, the sum . For example, the sum 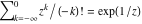 has an essential singularity at the point has an essential singularity at the point 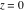 . . Puiseux series The , first studied by V.-A. Puiseux in 1850, expand 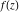 around a finite point around a finite point  as as  , with , with 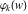 usually chosen as usually chosen as  . (Other choices for . (Other choices for 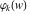 are possible through the use of iterated logarithms of the form are possible through the use of iterated logarithms of the form  , , 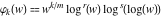 , and so on.) Choosing , and so on.) Choosing 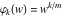 gives the Puiseux series for algebraic bivariate functions (because such functions should not include logarithms like gives the Puiseux series for algebraic bivariate functions (because such functions should not include logarithms like 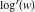 ). ). If this series contains only a finite number of nonzero coefficients  with negative indices with negative indices  , the point , the point  is an algebraic branch point of order is an algebraic branch point of order 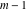 ; otherwise it is a transcendental branch point, such as the point ; otherwise it is a transcendental branch point, such as the point 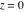 for the function for the function 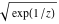 . . Puiseux series are widely used for describing solutions of differential equations near singular points and, in particular, for representations of elementary and special functions near their singular points. The named elementary functions can have rather complicated behaviors near their singular points. The point 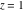 is an algebraic branch point of order 1 for the function is an algebraic branch point of order 1 for the function 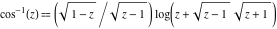 . This function has the Puiseux representation for its fundamental branch near point . This function has the Puiseux representation for its fundamental branch near point 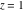 . . A similar representation occurs near the branch point 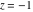 . . This expansion near the branch point 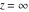 shows that shows that 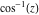 has a logarithmic-type singularity that can provide infinitely many values depending on the direction of approach of the variable has a logarithmic-type singularity that can provide infinitely many values depending on the direction of approach of the variable 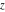 to ∞. to ∞. This Puiseux series for 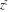 near the point near the point 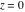 includes powers of logarithmic functions. includes powers of logarithmic functions. The Puiseux series for 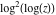 near the point near the point 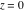 coincides with itself. coincides with itself. This Puiseux series for the ProductLog function 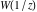 near the point near the point 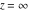 has a more complicated structure involving iterated logarithms. The complicated structure is to be expected from inverse functions like ProductLog. has a more complicated structure involving iterated logarithms. The complicated structure is to be expected from inverse functions like ProductLog. q-series This q‐series is widely used in applications. In the case 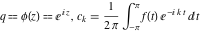 , it coincides with exponential Fourier series. , it coincides with exponential Fourier series. In very particular cases, q‐series can coincide with some trigonometric functions. For example, if 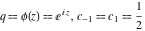 , and all other , and all other  are zero, then are zero, then 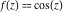 . . In more complicated cases, q‐series can define different special functions, for example elliptic theta functions: Dirichlet series General Dirichlet series If all coefficients 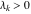 , this Dirichlet series for the function , this Dirichlet series for the function 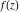 converges in some open half-plane converges in some open half-plane 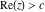 . In this case, for many Dirichlet series the abscissa of absolute convergence can be found by the formula . In this case, for many Dirichlet series the abscissa of absolute convergence can be found by the formula 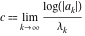 . . In the more general case 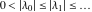 , the Dirichlet series absolutely converges in some open convex domain. In both cases, the sum of the Dirichlet series is an analytic function in the domain of convergence. , the Dirichlet series absolutely converges in some open convex domain. In both cases, the sum of the Dirichlet series is an analytic function in the domain of convergence. For example, if 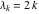 and and 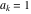 or or 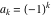 , you have, respectively, the Dirichlet series: , you have, respectively, the Dirichlet series: In the case 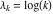 , you have the ordinary Dirichlet series , you have the ordinary Dirichlet series 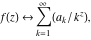 which in its simplest case ( which in its simplest case (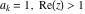 ) is the Riemann zeta function ) is the Riemann zeta function 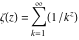 . Other interesting examples of the Dirichlet series include the series for elliptic theta functions. For instance, if . Other interesting examples of the Dirichlet series include the series for elliptic theta functions. For instance, if 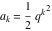 and and 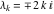 , you have the representations: , you have the representations: Generalized Fourier series Under some additional conditions (such as piecewise differentiability), this Fourier series of an arbitrary function 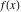 by the orthogonal system by the orthogonal system 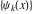 with Fourier coefficients with Fourier coefficients 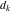 converges to converges to 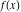 on an interval on an interval  at the points of continuity of at the points of continuity of 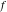 , and to , and to 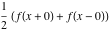 at the points of discontinuity of at the points of discontinuity of 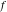 , where , where  ). ). The inequality takes place for all orthogonal systems 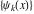 ; it is called Bessel's inequality. If it can be transformed into Parseval's equality: ; it is called Bessel's inequality. If it can be transformed into Parseval's equality: The corresponding system 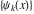 is called the complete system. is called the complete system. The best-known examples of orthogonal systems are the classical orthogonal polynomials and the trigonometric system including 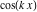 and and 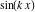 . . Generalized Fourier series through classical orthogonal polynomials For example, any sufficiently smooth function 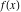 can be expanded in the Hermite orthogonal system can be expanded in the Hermite orthogonal system 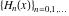 or in other orthogonal systems with corresponding weight factors as a generalized Fourier series, with its sum converging to or in other orthogonal systems with corresponding weight factors as a generalized Fourier series, with its sum converging to 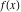 almost everywhere in corresponding intervals of variable almost everywhere in corresponding intervals of variable 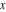 . The following represents this type of Fourier expansion through all classical orthogonal systems of polynomials. . The following represents this type of Fourier expansion through all classical orthogonal systems of polynomials. Exponential Fourier series This exponential Fourier series expansion can be transformed into a trigonometric Fourier series by using the Euler formula 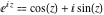 . . Following is an example of the exponential Fourier series for the simple function 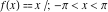 . . Outside the interval 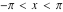 , the sum forms a periodic function and the following expansion holds for all real , the sum forms a periodic function and the following expansion holds for all real 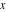 : : Trigonometric Fourier series This series expansion into a trigonometric system first appeared in an 1807 paper of J. Fourier, who used a similar expansion on the interval 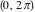 . However, L. Euler had discovered similar formulas for Fourier coefficients in 1777. . However, L. Euler had discovered similar formulas for Fourier coefficients in 1777. An arbitrary interval 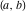 can be transformed into the interval can be transformed into the interval 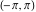 by changing the variable by changing the variable 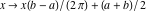 . This allows you to write the following Fourier series expansion of the arbitrary function . This allows you to write the following Fourier series expansion of the arbitrary function 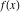 on an arbitrary interval on an arbitrary interval 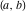 : : In the preceding formulas the coefficients should vanish at infinity 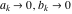 as as 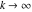 . . In the internal points 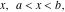 where the piecewise differentiable function where the piecewise differentiable function 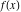 is continuous, the preceding sum of the Fourier series is equal to is continuous, the preceding sum of the Fourier series is equal to  and you can change the symbol ↔ to ⩵. and you can change the symbol ↔ to ⩵. At the points of discontinuity, this Fourier sum is equal to 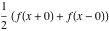 . . Outside the interval 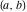 , the Fourier sum is a periodic function with period , the Fourier sum is a periodic function with period 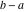 , but the behavior of this sum is not necessarily related to the actual behavior of the function , but the behavior of this sum is not necessarily related to the actual behavior of the function  outside the interval of expansion outside the interval of expansion 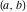 . . For example, let 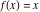 and and 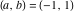 . Then . Then  , and: , and: Inspection shows that the Fourier sum 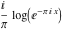 has period 2 and coincides with has period 2 and coincides with  on the interval on the interval 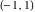 . But at the endpoint . But at the endpoint 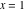 the Fourier sum is equal to 0, since you are evaluating the Fourier sum is equal to 0, since you are evaluating 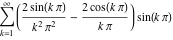 with with 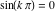 . This result coincides with . This result coincides with  . . Asymptotic series expansions Expansions at z==ComplexInfinity This asymptotic series expansion of the function  at at 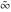 includes the main term includes the main term  and other terms of the form and other terms of the form 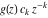 . The corresponding formal asymptotic series . The corresponding formal asymptotic series  is, by definition, formed in such a way that the following inequality holds for all is, by definition, formed in such a way that the following inequality holds for all 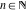 and sufficiently large and sufficiently large 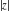 : : 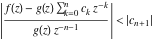 . This asymptotic series can be a divergent or convergent series. If this series converges, it coincides with the Taylor power series expansion at infinity. . This asymptotic series can be a divergent or convergent series. If this series converges, it coincides with the Taylor power series expansion at infinity. For example, the confluent hypergeometric function 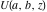 has the following asymptotic series expansion through the divergent series has the following asymptotic series expansion through the divergent series 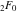 : : The relation takes place because the following inequality holds for each  and sufficiently large and sufficiently large  : : The function 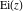 has a rather interesting asymptotic expansion at has a rather interesting asymptotic expansion at 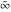 through the following divergent series: through the following divergent series: The next example includes a convergent series in an asymptotic expansion. So, you can use the sign ⩵ instead of ∝: In the particular case 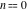 , the first generic formula for asymptotic expansion can be rewritten in the following form: , the first generic formula for asymptotic expansion can be rewritten in the following form: Expansions at z==z0 This asymptotic series expansion of the function 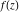 at at 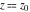 includes the main term includes the main term 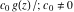 and other terms and other terms 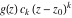 . The corresponding formal asymptotic series . The corresponding formal asymptotic series 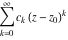 by definition is formed in such a way that the following inequality holds for all by definition is formed in such a way that the following inequality holds for all 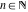 and sufficiently small and sufficiently small 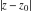 : : 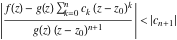 . This asymptotic series can be a divergent or convergent series. If this series converges, it coincides with the Taylor power series expansion at the point . This asymptotic series can be a divergent or convergent series. If this series converges, it coincides with the Taylor power series expansion at the point 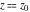 . . For example, the functions 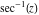 and and 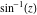 have the following asymptotic expansions near the points have the following asymptotic expansions near the points 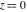 and and 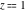 through convergent series. So, you can use the sign ⩵ instead of ∝ here: through convergent series. So, you can use the sign ⩵ instead of ∝ here: In the particular case 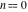 , the first generic formula for asymptotic expansion can be rewritten in the following form: , the first generic formula for asymptotic expansion can be rewritten in the following form: Residue representations For many analytic functions 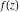 , you can establish so-called residue representations through infinite sums of residues of another analytic function , you can establish so-called residue representations through infinite sums of residues of another analytic function 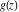 in the points in the points 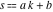 . The residue of the analytic function . The residue of the analytic function 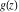 in the pole of order in the pole of order 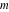 can be calculated by the formula: can be calculated by the formula: If the function 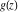 can be represented as a quotient can be represented as a quotient 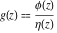 , where the functions , where the functions 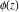 and and 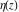 are analytic at the point are analytic at the point 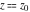 and and 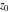 is the simple root of the equation is the simple root of the equation 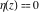 , then the following formula holds: , then the following formula holds: Very often, residue representations appear from the theory of the Meijer G function. The majority of functions of the hypergeometric type can be equivalently defined as corresponding to infinite sums of residues from products of ratios of gamma functions 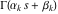 on power function on power function 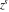 . . For example, the following residue representation formula for a logarithm function takes place: |