Low-order differentiation Derivatives of the first order This limit defines the derivative of a function 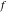 at the point at the point 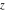 , if it exists. , if it exists. This formula reflects the property that a constant factor can be pulled out of the differentiation. This formula reflects the property that the derivative of a sum (and difference) is equal to the sum (and difference) of the derivatives. The product rule for differentiation shows that the derivative of a product is equal to the derivative of the first function multiplied by the second function plus the derivative of the second function multiplied by the first function. The product rule for differentiation shows how to evaluate the derivative of the product of three functions. The product rule for differentiation shows how to evaluate the derivative of the product of 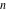 functions. functions. The quotient rule for differentiation shows that the derivative of the ratio is equal to the derivative of the numerator multiplied by the denominator minus the derivative of the denominator multiplied by the numerator, divided by the square of the denominator. The quotient rule for differentiation has been generalized to the case when the numerator is the product of two functions. The quotient rule for differentiation is generalized to the case when the denominator is the product of two functions. This formula shows that the derivative of the sum is equal to the sum of the derivatives. For an infinite sum it is true under some restrictions on 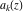 , which ensure the convergence of the series. , which ensure the convergence of the series. This formula shows that the derivative of a power series is equal to the corresponding sum of the derivatives. It is true inside the corresponding circle of convergence with radius 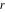 . . This chain rule for differentiation shows that the derivative of composition 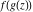 is equal to the derivative of the outer function is equal to the derivative of the outer function 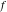 in the point in the point 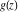 , multiplied by the derivative of the inner function , multiplied by the derivative of the inner function 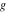 . . This chain rule for partial differentiation generalizes the previous chain rule for differentiation in the case of a function with two variables  . . This chain rule for partial differentiation generalizes the chain rule for differentiation in the case of a function with several variables 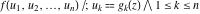 . . This formula shows that the derivative of the inverse function 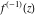 is equal to the reciprocal of the derivative of the direct function is equal to the reciprocal of the derivative of the direct function 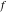 in the point in the point 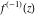 . . This formula shows that the composition of the first derivatives is equal to the derivative of the second order. This formula shows that the derivative of an indefinite integral produces the original function (the derivative is the inverse operation to the indefinite integration). This formula shows that the derivative of a definite integral with respect to the upper limit produces the original function. This formula shows that the derivative of a definite integral with respect to the low limit gives the original function with a negative sign. This formula shows that the order of differentiation and definite integration can be changed if the limits of the integral do not depend on the variable of differentiation. This formula reflects the general rule of differentiating an integral when its limits and its integrand depend on the variable of differentiation. Derivatives of the second order This limit defines the second derivative of a function 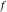 at the point at the point 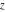 , if it exists. , if it exists. This formula shows how to evaluate the second derivative of a general composition 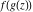 . . Symbolic differentiation Definition This limit defines the 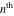 -order derivative of a function -order derivative of a function 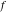 at the point at the point 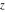 , if it exists. , if it exists. Converting to finite differences and back Products This rule is called the binomial differentiation rule for the 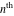 -order derivative. -order derivative. This rule is called the multinomial differentiation rule for the 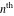 -order derivative. -order derivative. This rule is called the multinomial differentiation rule for the 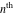 -order derivative. -order derivative. Ratios This formula shows how to evaluate an 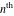 -order derivative for the quotient of two functions. -order derivative for the quotient of two functions. This formula shows how to evaluate an 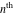 -order derivative for the quotient of two functions. -order derivative for the quotient of two functions. This formula shows how to evaluate an 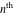 -order derivative for the quotient of two functions. -order derivative for the quotient of two functions. This formula shows how to evaluate an  -order derivative for the quotient of two functions. -order derivative for the quotient of two functions. Power This formula shows how to evaluate an 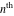 -order derivative of the power -order derivative of the power  . . This formula shows how to evaluate an 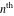 -order derivative of the power -order derivative of the power  . . This formula shows how to evaluate an 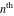 -order derivative of the power -order derivative of the power 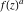 . . This formula shows how to evaluate an 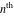 -order derivative of the power -order derivative of the power 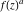 . . Positive integer powers This formula shows how to evaluate an  -order derivative of the square -order derivative of the square 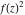 . . This formula shows how to evaluate an 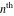 -order derivative of the square -order derivative of the square 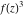 . . This formula shows how to evaluate an 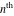 -order derivative of the cube -order derivative of the cube  . . This formula shows how to evaluate an 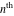 -order derivative of the fourth power -order derivative of the fourth power  . . This formula shows how to evaluate an  -order derivative of the fourth power -order derivative of the fourth power 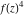 . . This formula shows how to evaluate an 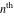 -order derivative of the general integer power -order derivative of the general integer power 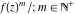 . . This formula shows how to evaluate an 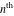 -order derivative of the general integer power -order derivative of the general integer power  . . Negative integer powers This formula shows how to evaluate an  -order derivative of the reciprocal -order derivative of the reciprocal 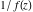 . . This formula shows how to evaluate an 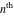 -order derivative of the reciprocal -order derivative of the reciprocal 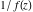 . . This formula shows how to evaluate an 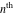 -order derivative of the reciprocal -order derivative of the reciprocal 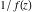 . . This formula shows how to evaluate an 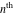 -order derivative of the reciprocal -order derivative of the reciprocal 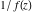 . . Log from function This formula shows how to evaluate an 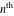 -order derivative of the composition with logarithm -order derivative of the composition with logarithm 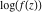 . . This formula shows how to evaluate an 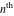 -order derivative of the composition with logarithm -order derivative of the composition with logarithm 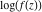 . . This formula shows how to evaluate an  -order derivative of the composition with logarithm -order derivative of the composition with logarithm 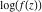 . . Exp from function This formula shows how to evaluate an 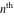 -order derivative of the composition with exponential function -order derivative of the composition with exponential function 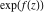 . . This formula shows how to evaluate an 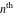 -order derivative of the composition with exponential function -order derivative of the composition with exponential function 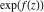 . . This formula shows how to evaluate an 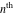 -order derivative of the composition with exponential function -order derivative of the composition with exponential function 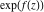 . . This formula shows how to evaluate an  -order derivative of the composition with exponential function -order derivative of the composition with exponential function 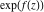 . . This formula shows how to evaluate an 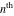 -order derivative of the composition with exponential function -order derivative of the composition with exponential function  . . Function from power This formula shows how to evaluate an 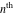 -order derivative of the composition with power function -order derivative of the composition with power function 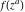 . . This formula shows how to evaluate an 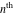 -order derivative of the composition -order derivative of the composition  . . This formula shows how to evaluate the derivative of the  -order of the composition -order of the composition 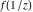 . . This formula shows how to evaluate an 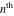 -order derivative of the composition -order derivative of the composition  . . Function from exponent This formula shows how to evaluate an 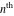 -order derivative of the composition -order derivative of the composition 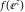 . . This formula shows how to evaluate an  -order derivative of the composition -order derivative of the composition 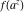 . . This formula shows how to evaluate an 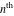 -order derivative of the composition -order derivative of the composition 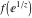 . . This formula shows how to evaluate an 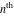 -order derivative of the composition -order derivative of the composition 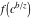 . . This formula shows how to evaluate an 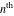 -order derivative of the composition -order derivative of the composition 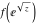 . . This formula shows how to evaluate an 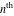 -order derivative of the composition -order derivative of the composition  . . This formula shows how to evaluate an 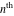 -order derivative of the composition -order derivative of the composition 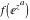 . . This formula shows how to evaluate an 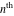 -order derivative of the composition -order derivative of the composition 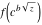 . . This formula shows how to evaluate an 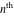 -order derivative of the composition -order derivative of the composition 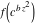 . . This formula shows how to evaluate an  -order derivative of the composition -order derivative of the composition  . . Function from trigonometric functions This formula shows how to evaluate an  -order derivative of the composition -order derivative of the composition 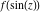 . . This formula shows how to evaluate an  -order derivative of the composition -order derivative of the composition 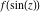 . . This formula shows how to evaluate an 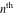 -order derivative of the composition -order derivative of the composition 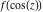 . . This formula shows how to evaluate an 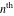 -order derivative of the composition -order derivative of the composition 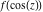 . . Function from hyperbolic functions This formula shows how to evaluate an 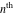 -order derivative of the composition -order derivative of the composition 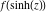 . . This formula shows how to evaluate an 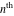 -order derivative of the composition -order derivative of the composition 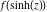 . . This formula shows how to evaluate an 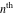 -order derivative of the composition -order derivative of the composition  . . This formula shows how to evaluate an 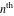 -order derivative of the composition -order derivative of the composition 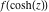 . . General compositions This formula shows how to evaluate an 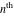 -order derivative of the general composition -order derivative of the general composition 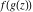 . . This formula shows how to evaluate an 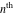 -order derivative of the general composition -order derivative of the general composition 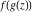 . . This formula is called . This formula, , shows how to evaluate an 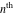 -order derivative of the general composition -order derivative of the general composition 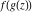 . . This formula shows how to evaluate an 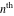 -order derivative of the general composition -order derivative of the general composition 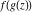 . . General power exponential compositions This formula shows how to evaluate an  -order derivative of the general power exponential composition -order derivative of the general power exponential composition 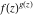 . . This formula shows how to evaluate an 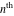 -order derivative of the general power exponential composition -order derivative of the general power exponential composition 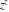 . . Inverse function This formula shows how to evaluate an 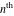 -order derivative of the inverse function -order derivative of the inverse function 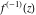 . . Repeated derivatives This formula shows how to apply  times the operation times the operation 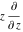 to the function to the function 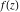 . . This formula shows how to apply 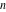 times the operation times the operation 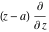 to the function to the function 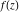 . . Fractional integro-differentiation The 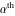 fractional integro‐derivative of the function fractional integro‐derivative of the function  with respect to with respect to 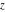 is defined by the preceding formula, where the integration in Mathematica should be performed with the option GenerateConditions->False: Integrate[f[t](z-t)α+n-1Gamma[α+n],{t,0,z},GenerateConditionsFalse. This definition supports the Riemann‐Liouville‐Hadamard fractional left‐sided integro‐differentiation at the point 0. is defined by the preceding formula, where the integration in Mathematica should be performed with the option GenerateConditions->False: Integrate[f[t](z-t)α+n-1Gamma[α+n],{t,0,z},GenerateConditionsFalse. This definition supports the Riemann‐Liouville‐Hadamard fractional left‐sided integro‐differentiation at the point 0. This formula for the 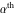 fractional integro‐derivative represents the fractional integral of the function fractional integro‐derivative represents the fractional integral of the function 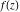 with respect to with respect to 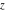 . This integral is called the . . This integral is called the . This formula for the  fractional integro‐derivative actually represents the fractional derivative of the function fractional integro‐derivative actually represents the fractional derivative of the function  with respect to with respect to  . This derivative includes the composition of the corresponding usual . This derivative includes the composition of the corresponding usual  derivative of order derivative of order 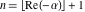 and an Abel integral. and an Abel integral. This formula shows how to evaluate the 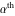 fractional integro‐derivative of the analytical function near the point fractional integro‐derivative of the analytical function near the point 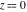 . . This formula shows how to evaluate the 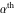 fractional integro‐derivative of a function having Laurent series expansion, multiplied on fractional integro‐derivative of a function having Laurent series expansion, multiplied on 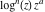 near the point near the point 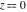 . . This formula shows that for the evaluation of the  fractional integro‐derivative of the analytical function fractional integro‐derivative of the analytical function 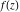 near the point near the point 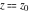 , you need to re-expand this function in a series near the point , you need to re-expand this function in a series near the point 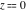 and then evaluate the corresponding integro‐derivative. and then evaluate the corresponding integro‐derivative. |