|
Introduction to the GCD and LCM (greatest common divisor and least common multiple)
General
The legendary Greek mathematician Euclid (ca. 325–270 BC) suggested an algorithm for finding the greatest common divisor of two integers, which was later named the Euclidean algorithm. This algorithm, as well as computationally refined versions, are in widespread use today.
Definitions of GCD and LCM
The GCD and LCM group of functions includes the following three functions:
• the greatest common divisor (gcd): 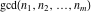 • the least common multiple (lcm):
• the least common multiple (lcm): 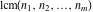 • the extended greatest common divisor (egcd):
• the extended greatest common divisor (egcd): 
These functions are defined in the following ways:
 is the greatest common divisor of the integers (or rational) is the greatest common divisor of the integers (or rational) 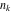 . It is the greatest integer factor common to all the . It is the greatest integer factor common to all the 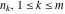 . .
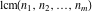 is the least common multiple of the integers (or rational) is the least common multiple of the integers (or rational) 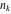 . It is the minimal positive integer that divides all the . It is the minimal positive integer that divides all the 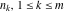 . .
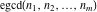 is the extended greatest common divisor of the integers is the extended greatest common divisor of the integers 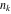 . In particular, . In particular, 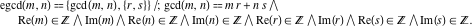
Examples:
The greatest common divisor of 21 and 48, 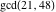 is 3. Similar examples are is 3. Similar examples are 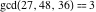 , , 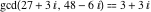 , , 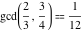 .
The least common multiple of the three numbers 2, 4, and 5, .
The least common multiple of the three numbers 2, 4, and 5,  is is 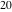 . Similar examples are . Similar examples are 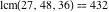 , ,  , ,  .
The extended greatest common divisor of 21 and 48 .
The extended greatest common divisor of 21 and 48 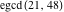 is is  because the greatest common divisor because the greatest common divisor 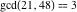 and and 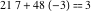 . Similarly, . Similarly, 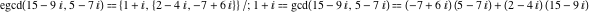 . .
Connections within the group of the GCD and LCM and with other function groups
Representations through equivalent functions
The functions  and and  satisfy the following interrelations: satisfy the following interrelations:
The best-known properties and formulas of the GCD and LCM
Specific values for specialized variables
The functions GCD and LCM  , ,  , and , and 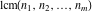 have the following values for specialized values: have the following values for specialized values:
The first values of the greatest common divisor (gcd(m, n)) of the integers 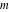 and and 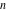 for for  and and 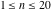 are described in the following table: are described in the following table:
The first values of the extended greatest common divisor ( ) of the integers ) of the integers 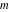 and and 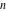 for for 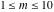 and and 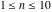 are described in the following table: are described in the following table:
The first values of the least common multiple (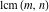 ) of the integers ) of the integers 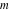 and and 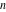 for for 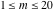 and and 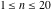 are described in the following table: are described in the following table:
Analyticity
The functions 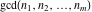 and and 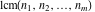 are nonanalytical functions defined over are nonanalytical functions defined over 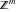 with values in with values in 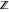 .
The function .
The function 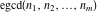 is a vector‐valued nonanalytical function defined over is a vector‐valued nonanalytical function defined over 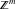 . .
Periodicity
All three functions 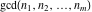 , ,  , and , and 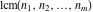 do not have periodicity. do not have periodicity.
Parity and symmetry
The functions 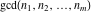 and and 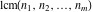 are even functions: are even functions:
The functions 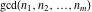 and and 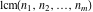 have permutation symmetry: have permutation symmetry:
Series representations
The function 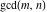 has the following sum representations: has the following sum representations:
where 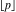 is the floor function and is the floor function and 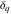 is the Kronecker delta function. is the Kronecker delta function.
Product representations
The functions 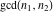 and and 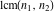 have the following product representations: have the following product representations:
Generating functions
The function 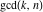 can be represented as the coefficients of the series expansion of corresponding generating functions, which includes a sum of the Euler totient function: can be represented as the coefficients of the series expansion of corresponding generating functions, which includes a sum of the Euler totient function:
Transformations with multiple arguments
The GCD and LCM functions 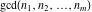 , , 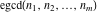 , and , and 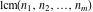 satisfy special relations including multiple arguments, for example: satisfy special relations including multiple arguments, for example:
Identities
The GCD and LCM functions satisfy some parallel identities that can be presented in the forms shown in the following table:
Summation
There are many finite and infinite sums containing GCD and LCM functions, for example:
Limit operation
The following two related limits include the function 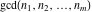 . The third limit includes lcm( . The third limit includes lcm(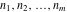 ): ):
Inequalities
The functions 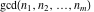 and and 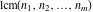 satisfy various inequalities, for example: satisfy various inequalities, for example:
Applications of the GCD and LCM
The GCD and LCM functions have numerous applications throughout mathematics, number theory, symbolic algorithms, and linear Diophantine equations.
|