|
Definitions of partitions
The partition functions discussed here include two basic functions that describe the structure of integer numbers—the number of unrestricted partitions of an integer (partitions P) 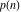 , and the number of partitions of an integer into distinct parts (partitions Q) , and the number of partitions of an integer into distinct parts (partitions Q) 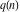 . .
Partitions P
For nonnegative integer 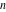 , the function , the function 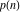 is the number of unrestricted partitions of the positive integer is the number of unrestricted partitions of the positive integer 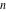 into a sum of strictly positive numbers that add up to into a sum of strictly positive numbers that add up to 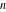 independent of the order, when repetitions are allowed. independent of the order, when repetitions are allowed.
The function 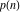 can be described by the following formulas: can be described by the following formulas:
where 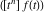 (with (with 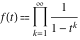 ) is the coefficient of the ) is the coefficient of the 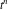 term in the series expansion around term in the series expansion around 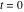 of the function of the function 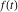 : : 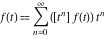 . .
Example: There are seven possible ways to express 5 as a sum of nonnegative integers: 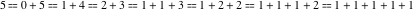 . For this reason . For this reason  . .
Partitions Q
For nonnegative integer 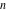 , the function , the function 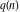 is the number of restricted partitions of the positive integer is the number of restricted partitions of the positive integer 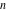 into a sum of distinct positive numbers that add up to into a sum of distinct positive numbers that add up to 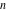 when order does not matter and repetitions are not allowed. when order does not matter and repetitions are not allowed.
The function 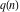 can be described by the following formulas: can be described by the following formulas:
where 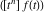 (with (with  ) is the coefficient of the ) is the coefficient of the 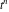 term in the series expansion around term in the series expansion around 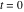 of the function of the function  : : 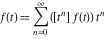 . .
Example: There are three possible ways to express 5 as a sum of nonnegative integers without repetitions: 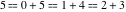 . For this reason . For this reason 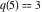 . .
|