|
The best-known properties and formulas of partitions
Simple values at zero and infinity
The partition functions 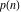 and and  are defined for zero and infinity values of argument are defined for zero and infinity values of argument 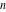 by the following rules: by the following rules:
Specific values for specialized variables
The following table represents the values of the partitions 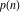 and and 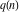 for for 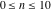 and some powers of 10: and some powers of 10:
Analyticity
The partition functions  and and 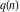 are non‐analytical functions that are defined only for integers. are non‐analytical functions that are defined only for integers.
Periodicity
The partition functions 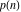 and and 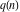 do not have periodicity. do not have periodicity.
Parity and symmetry
The partition functions  and and 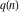 do not have symmetry. do not have symmetry.
Series representations
The partition functions 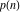 and and  have the following series representations: have the following series representations:
where 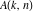 is a special case of a generalized Kloosterman sum: is a special case of a generalized Kloosterman sum:
Asymptotic series expansions
The partition functions 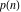 and and 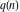 have the following asymptotic series expansions: have the following asymptotic series expansions:
Generating functions
The partition functions 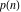 and and 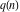 can be represented as the coefficients of their generating functions: can be represented as the coefficients of their generating functions:
where 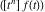 is the coefficient of the is the coefficient of the 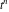 term in the series expansion around term in the series expansion around 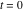 of the function of the function 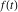 , ,  . .
Identities
The partition functions 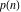 and and  satisfy numerous identities, for example: satisfy numerous identities, for example:
Complex characteristics
As real valued functions, the partitions 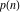 and and  have the following complex characteristics: have the following complex characteristics:
Summation
There exist just a few formulas including finite and infinite summation of partitions, for example:
Inequalities
The partitions 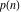 and and 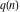 satisfy various inequalities, for example: satisfy various inequalities, for example:
Congruence properties
The 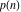 partitions have the following congruence properties: partitions have the following congruence properties:
Zeros
The 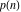 and and 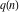 partitions have the following unique zeros: partitions have the following unique zeros:
|