|
For all possible values of their arguments, the discrete delta functions 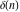 and and 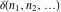 , Kronecker delta functions , Kronecker delta functions  and and 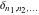 , and signature (Levi–Civita symbol) , and signature (Levi–Civita symbol) 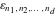 are defined by the formulas: are defined by the formulas:
In other words, the Kronecker delta function is equal to 1 if all its arguments are equal.
In the case of one variable, the discrete delta function 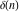 coincides with the Kronecker delta function coincides with the Kronecker delta function 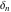 . In the case of several variables, the discrete delta function . In the case of several variables, the discrete delta function 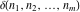 coincides with Kronecker delta function coincides with Kronecker delta function 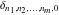 : :
where 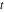 is the number of permutations needed to go from the sorted version of is the number of permutations needed to go from the sorted version of 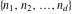 to to 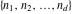 . .
|