The set of natural numbers 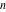 : : 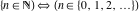 . . 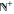
The set of positive natural numbers 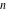 : : 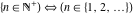 . . 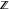
The set of integer numbers 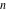 : : 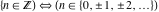 . . 
The set of rational numbers 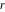 : : 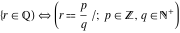 . . 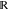
The set of real numbers 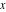 : : 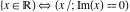 . . 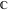
The set of complex numbers 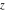 : : 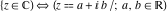 . . 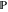
The set of prime numbers 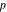 : : 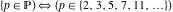 . . 
The empty set. 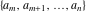
The finite set of elements 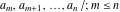 . . 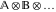
The Cartesian product of the sets 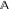 , , 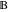 , …. , …. 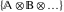
The ordered set of sets 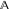 , , 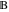 ,…. ,….
As a rule, the following notation style is supported for all variables, numbers, and indices.
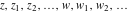
Generic complex variables. 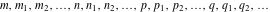
Integer variables. 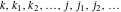
Dummy variables used in sums and products. 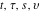
Integration dummy variables in definite integrals or integral transforms.
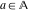
The element 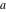 does belong to the set does belong to the set 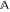 . . 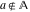
The element 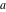 does not belong to the set does not belong to the set 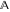 . . 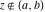
The number 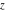 does not belong to the specified interval does not belong to the specified interval  . .
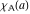
The characteristic function of a set 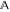 has the value 1 when its argument has the value 1 when its argument 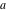 is an element of the specified set 𝔸, and the value 0 otherwise. is an element of the specified set 𝔸, and the value 0 otherwise. 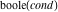
Gives 1 if cond is true, and 0 if it is false. 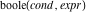
Gives expr if cond is true, and 0 otherwise. |