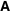
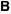
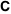
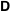
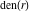
The denominator of 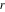 . .
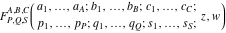
The generalized hypergeometric function of two variables (Kampe de Feriet function): 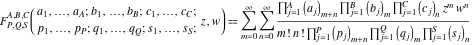 . . 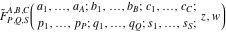
The regularized generalized hypergeometric function of two variables (regularized Kampe de Feriet function): 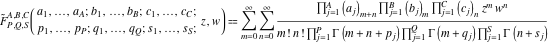 . . 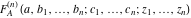
The Lauricella function A of 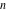 variables: variables: 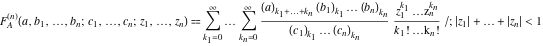 . . 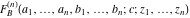
The Lauricella function B of 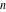 variables: variables: 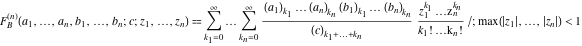 . . 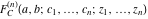
The Lauricella function C of 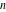 variables: variables: 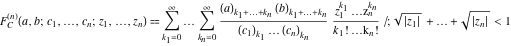 . . 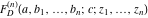
The Lauricella function D of 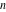 variables: variables: 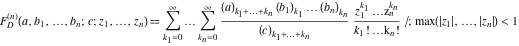 . .
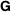
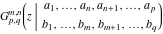
The Meijer G function: 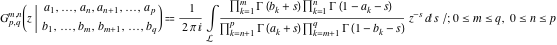 . . The infinite contour of integration  separates the poles of separates the poles of 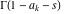 at at 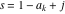 , , 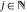 from the poles of from the poles of 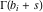 at at 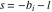 , , 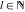 . Such a contour always exists in the cases . Such a contour always exists in the cases 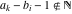 . . There are three possibilities for the contour 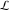 : : (i) 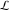 runs from γ-ⅈ ∞ to γ+ⅈ ∞ (where runs from γ-ⅈ ∞ to γ+ⅈ ∞ (where 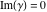 ) so that all poles of ) so that all poles of 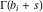 , , 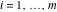 are to the left of are to the left of 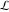 , and all poles of , and all poles of 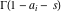 , , 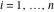 are to the right of ℒ. This contour can be a straight line are to the right of ℒ. This contour can be a straight line 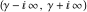 if if 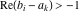 (then (then 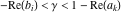 ). (In this case, the integral converges if ). (In this case, the integral converges if 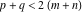 , , 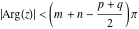 . If . If 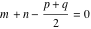 , then , then 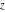 must be real and positive and the additional condition must be real and positive and the additional condition 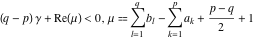 should be added.) should be added.) (ii) 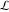 is a left loop, starting and ending at -∞ and encircling all poles of is a left loop, starting and ending at -∞ and encircling all poles of 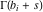 , ,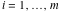 , once in the positive direction, but none of the poles of , once in the positive direction, but none of the poles of 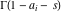 , , 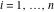 . In this case, the integral converges if . In this case, the integral converges if 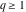 and one of the following conditions is satisfied: and one of the following conditions is satisfied: ◼ 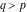 or or 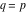 and and 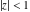 ◼ 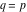 and and 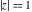 and and 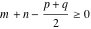 and and 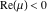 . . (iii) 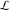 is a right loop, starting and ending at +∞ and encircling all poles of is a right loop, starting and ending at +∞ and encircling all poles of 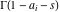 , , 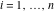 , once in the negative direction, but none of the poles of , once in the negative direction, but none of the poles of 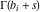 , , 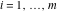 . In this case, the integral converges if . In this case, the integral converges if 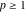 and one of the following conditions is satisfied: and one of the following conditions is satisfied: ◼ 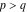 or or 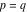 and and 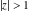 ◼ 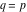 and and 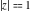 and and 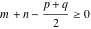 and and 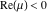 . . Identities containing MeijerG

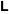
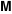
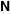
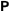
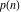
The number of unrestricted partitions (independent of the order and with repetitions allowed) of the positive integer 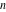 into a sum of strictly positive integers that add up to into a sum of strictly positive integers that add up to 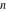 : : 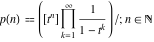 . . Identities containing PartitionsP 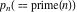
The 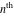 prime number (the smallest integer greater than prime number (the smallest integer greater than 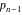 that cannot be divided by any integer greater than 1 and smaller than itself): that cannot be divided by any integer greater than 1 and smaller than itself): 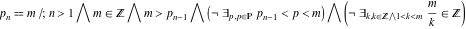 . . Identities containing Prime 
A Boolean function that tests whether the angular momentum quantum numbers are physically realizable: 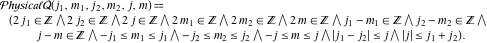
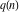
The number of ordered partitions (independent of the order and no repetitions allowed) of the positive integer 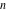 into a sum of strictly positive integers which add up to into a sum of strictly positive integers which add up to 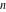 : : 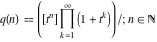 . . Identities containing PartitionsQ
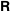
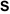
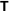
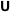
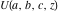
The Gauss type hypergeometric function 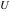 : : 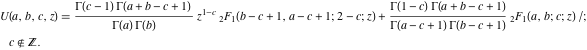
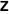
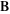
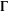
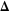
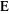
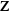
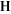
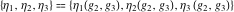
The values of the Weierstrass zeta function at the half-periods 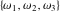 : : 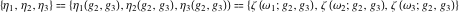 . .
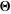
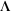
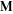
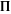
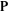
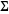
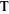
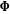
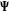
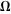
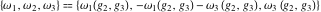
The half‐periods for Weierstrass elliptic functions corresponding to the invariants 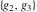 : :
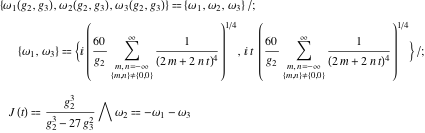
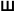
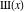
The generalized Dirac comb function Ш(x): 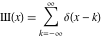 . . |