|
Introduction to the Arithmetic‐Geometric Mean
General
The arithmetic-geometric mean appeared in the works of J. Landen (1771, 1775) and J.‐L. Lagrange (1784-1785) who defined it through the following quite‐natural limit procedure:
C. F. Gauss (1791–1799, 1800, 1876) continued to research this limit and in 1800 derived its representation through the hypergeometric function 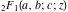 . .
Definition of arithmetic-geometric mean
The arithmetic-geometric mean 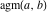 is defined through the reciprocal value of the complete elliptic integral is defined through the reciprocal value of the complete elliptic integral 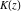 by the formula: by the formula:
A quick look at the arithmetic-geometric mean Here is a quick look at the graphic for the arithmetic‐geometric mean over the real 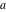 – –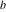 ‐plane. ‐plane.
Connections within the arithmetic-geometric mean group and with other function groups
Representations through more general functions
The arithmetic‐geometric mean 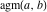 can be represented through the reciprocal function of the particular cases of hypergeometric and Meijer G functions: can be represented through the reciprocal function of the particular cases of hypergeometric and Meijer G functions:
Representations through related equivalent functions
The definition of the arithmetic‐geometric mean 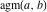 can be interpreted as a representation of can be interpreted as a representation of  through related equivalent functions—the reciprocal of the complete elliptic integral through related equivalent functions—the reciprocal of the complete elliptic integral 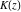 with with 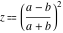 : :
The best-known properties and formulas for the arithmetic-geometric mean
Values in points
The arithmetic‐geometric mean  can be exactly evaluated in some points, for example: can be exactly evaluated in some points, for example:
Real values for real arguments
For real values of arguments  , ,  (with (with 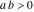 ), the values of the arithmetic‐geometric mean ), the values of the arithmetic‐geometric mean 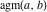 are real. are real.
Analyticity
The arithmetic‐geometric mean 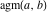 is an analytical function of is an analytical function of 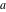 and and  that is defined over that is defined over 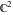 . .
Poles and essential singularities
The arithmetic‐geometric mean 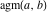 does not have poles and essential singularities. does not have poles and essential singularities.
Branch points and branch cuts
The arithmetic‐geometric mean  on the on the 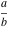 ‐plane has two branch points: ‐plane has two branch points:  . It is a single‐valued function on the . It is a single‐valued function on the 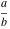 ‐plane cut along the interval ‐plane cut along the interval 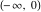 , where it is continuous from above: , where it is continuous from above:
Periodicity
The arithmetic‐geometric mean 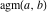 does not have periodicity. does not have periodicity.
Parity and symmetries
The arithmetic‐geometric mean 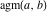 is an odd function and has mirror and permutation symmetry: is an odd function and has mirror and permutation symmetry:
The arithmetic‐geometric mean  is the homogenous function: is the homogenous function:
Series representations
The arithmetic‐geometric mean 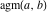 has the following series representations at the points has the following series representations at the points 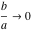 , , 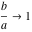 , and , and  : :
Product representation
The arithmetic‐geometric mean  has the following infinite product representation: has the following infinite product representation:
Integral representation
The arithmetic‐geometric mean  has the following integral representation: has the following integral representation:
Limit representation
The arithmetic‐geometric mean  has the following limit representation, which is often used for the definition of has the following limit representation, which is often used for the definition of 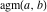 : :
Transformations
The homogeneity property of the arithmetic‐geometric mean 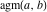 leads to the following transformations: leads to the following transformations:
Another group of transformations is based on the first of the following properties:
Representations of derivatives
The first derivatives of the arithmetic‐geometric mean 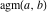 have rather simple representations: have rather simple representations:
The 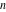 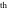 -order symbolic derivatives are much more complicated. Here is an example: -order symbolic derivatives are much more complicated. Here is an example:
Differential equations
The arithmetic‐geometric mean 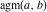 satisfies the following second-order ordinary nonlinear differential equation: satisfies the following second-order ordinary nonlinear differential equation:
It can also be represented as partial solutions of the following partial differential equation:
Inequalities
The arithmetic‐geometric mean 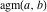 lies between the middle geometric mean and middle arithmetic mean, which is shown in the following famous inequality: lies between the middle geometric mean and middle arithmetic mean, which is shown in the following famous inequality:
Applications of the arithmetic-geometric mean
Applications of the arithmetic‐geometric mean include fast high‐precision computation of 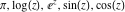 , and so on. , and so on.
|