|
Connections within the group of elliptic exp and elliptic log and with other function groups
Representations through more general functions
The elliptic logarithm 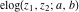 is the particular case of the hypergeometric function of two variables (Appell function is the particular case of the hypergeometric function of two variables (Appell function 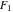 ): ):
Representations through related equivalent functions
The elliptic exponent 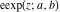 is connected with Jacobi amplitude by the following formula: is connected with Jacobi amplitude by the following formula:
The elliptic exponent 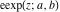 and elliptic logarithm and elliptic logarithm 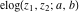 can be expressed through direct and inverse Weierstrass functions by the following formulas: can be expressed through direct and inverse Weierstrass functions by the following formulas:
The elliptic logarithm 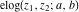 has the following representation through incomplete elliptic integral has the following representation through incomplete elliptic integral 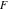 : :
Relations to inverse functions
The elliptic logarithm  is the inverse function to the elliptic exponent is the inverse function to the elliptic exponent 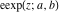 and its derivative and its derivative 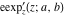 . Relations between them are described by the following formulas: . Relations between them are described by the following formulas:
|