|
The best-known properties and formulas of the tensor functions
Simple values at zero and infinity
The tensor functions  , , 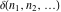 , , 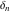 , and , and 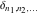 can have unit values at infinity: can have unit values at infinity:
Specific values for specialized variables
The tensor functions  , , 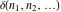 , , 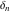 , , 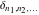 , and , and 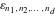 have the following values for some specialized variables: have the following values for some specialized variables:
Analyticity
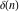 and and are nonanalytical functions defined over are nonanalytical functions defined over 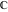 . Their possible values are . Their possible values are 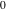 and and  . .
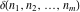 and and 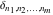 are nonanalytical functions defined over are nonanalytical functions defined over 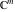 . Their possible values are . Their possible values are 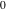 and and  . .
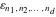 is a nonanalytical function, defined over the set of tuples of complex numbers with possible values is a nonanalytical function, defined over the set of tuples of complex numbers with possible values 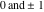 . .
Periodicity
The tensor functions 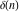 , , 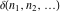 , , 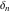 , , 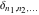 , and , and  do not have periodicity. do not have periodicity.
Parity and symmetry quasi-permutation symmetry
The tensor functions 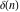 , , 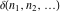 , , 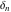 , and , and 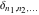 are even functions: are even functions:
The tensor functions 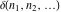 , , 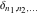 , and , and 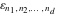 have permutation symmetry, for example: have permutation symmetry, for example:
Integral representations
The discrete delta function 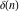 and Kronecker delta function and Kronecker delta function 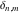 have the following integral representations along the interval have the following integral representations along the interval 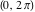 and unit circle and unit circle 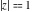 : :
Transformations
The tensor functions 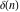 , ,  , ,  , , 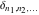 , and , and 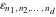 satisfy various identities, for example: satisfy various identities, for example:
Complex characteristics
The tensor functions 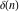 , ,  , , 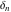 , , 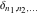 , and , and 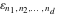 have the following complex characteristics: have the following complex characteristics:
Differentiation
Differentiation of the tensor functions  and and 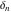 can be provided by the following formulas: can be provided by the following formulas:
Fractional integro‐differentiation of the tensor functions 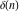 and and 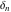 can be provided by the following formulas: can be provided by the following formulas:
Indefinite integration
Indefinite integration of the tensor functions 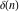 and and 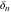 can be provided by the following formulas: can be provided by the following formulas:
Summation
The following relations represent the sifting properties of the Kronecker and discrete delta functions:
There exist various formulas including finite summation of signature 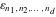 , for example: , for example:
|