|
The functions GCD and LCM  , ,  , and , and 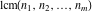 have the following values for specialized values: have the following values for specialized values:
The first values of the greatest common divisor (gcd(m, n)) of the integers  and and  for for  and and  are described in the following table: are described in the following table:
The first values of the extended greatest common divisor ( ) of the integers ) of the integers 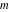 and and 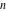 for for 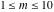 and and 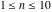 are described in the following table: are described in the following table:
The first values of the least common multiple (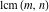 ) of the integers ) of the integers 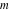 and and 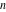 for for 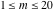 and and 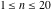 are described in the following table: are described in the following table:
The functions 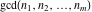 and and 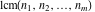 are nonanalytical functions defined over are nonanalytical functions defined over 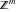 with values in with values in 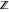 .
The function .
The function 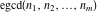 is a vector‐valued nonanalytical function defined over is a vector‐valued nonanalytical function defined over 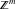 . .
All three functions 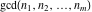 , ,  , and , and 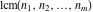 do not have periodicity. do not have periodicity.
The functions 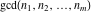 and and 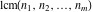 are even functions: are even functions:
The functions 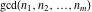 and and 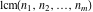 have permutation symmetry: have permutation symmetry:
The function 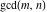 has the following sum representations: has the following sum representations:
where 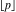 is the floor function and is the floor function and 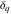 is the Kronecker delta function. is the Kronecker delta function.
The functions 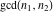 and and 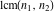 have the following product representations: have the following product representations:
The function 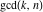 can be represented as the coefficients of the series expansion of corresponding generating functions, which includes a sum of the Euler totient function: can be represented as the coefficients of the series expansion of corresponding generating functions, which includes a sum of the Euler totient function:
The GCD and LCM functions 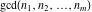 , , 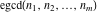 , and , and 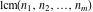 satisfy special relations including multiple arguments, for example: satisfy special relations including multiple arguments, for example:
The GCD and LCM functions satisfy some parallel identities that can be presented in the forms shown in the following table:
There are many finite and infinite sums containing GCD and LCM functions, for example:
The following two related limits include the function 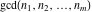 . The third limit includes lcm( . The third limit includes lcm(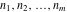 ): ):
The functions 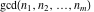 and and 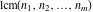 satisfy various inequalities, for example: satisfy various inequalities, for example:
|