|
Introduction to the Fibonacci and Lucas numbers
The sequence now known as Fibonacci numbers (sequence 0, 1, 1, 2, 3, 5, 8, 13...) first appeared in the work of an ancient Indian mathematician, Pingala (450 or 200 BC). Pingala's work with the mountain of cadence (now known as Pascal's triangle) made him the first known person to have looked into Fibonacci numbers. Next, another Indian mathematician, Virahanka (6th century AD), took note of the Fibonacci sequence through analysis of a completely different problem. Virahanka considered the following problem: assuming that lines of n units are composed of syllables that can be long or short—a long syllable takes twice as long as a short syllable to articulate—and each line of n units takes the same time to articulate no matter how it is composed, how many different combinations of syllables are there for each line of length n? Research of this question was continued by the Indian scholar Hemachandra and the Indian mathematician Gopala in the 12th century. Almost a half century later, the sequence was studied by the man whose name is most heavily linked to Fibonacci numbers, Leonardo of Pisa, a.k.a. Fibonacci (1202). Fibonacci considered the famous growth of an idealized rabbit population problem.
Later, European mathematicians began to study various aspects of Fibonacci numbers. Researchers included J. Kepler (1608), A. Girard (1634), R. Simpson (1753), É. Léger (1837), É. Lucas (1870, 1876–1880), G. H. Hardy, and E. M. Wright (1938). From this group, it was Francois Edouard Anatole Lucas (1870, 1876–1880) who gave Fibonacci numbers their name. He also investigated a similar sequence (sequence 2, 1, 3, 4, 7, 11, 18, 29, …), which was later coined Lucas numbers. In many works these sequences are notated 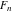 and and 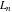 ( (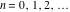 ) to represent the first letters of the last names Fibonacci and Lucas. Eventually, it was established that both sequences can be analytically extended on complex ) to represent the first letters of the last names Fibonacci and Lucas. Eventually, it was established that both sequences can be analytically extended on complex 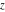 -planes and that they satisfy the same three‐term recurrence relation, reflecting that the Fibonacci and Lucas numbers are the sums of two neighboring terms: -planes and that they satisfy the same three‐term recurrence relation, reflecting that the Fibonacci and Lucas numbers are the sums of two neighboring terms:
For integer arguments, Fibonacci and Lucas numbers can be elegantly represented through the symmetric relations (including the golden ratio  ): ):
Definitions of the Fibonacci and Lucas numbers:
For any complex 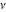 , the Fibonacci numbers , the Fibonacci numbers  and Lucas numbers and Lucas numbers 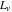 are defined by the formulas: are defined by the formulas:
where 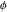 is the golden ratio is the golden ratio 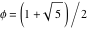 . .
Connections within the group of the Fibonacci and Lucas numbers and with other function groups
Representations through more general functions
The Fibonacci and Lucas numbers  and and 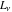 have the following representations through more general functions including some hypergeometric functions and Meijer G functions: have the following representations through more general functions including some hypergeometric functions and Meijer G functions:
Representations of Fibonacci and Lucas numbers through each other and through elementary functions
The Fibonacci and Lucas numbers 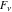 and and 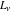 can be represented through each other by the following formulas: can be represented through each other by the following formulas:
The Fibonacci and Lucas numbers 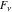 and and 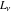 have the following representations through elementary functions: have the following representations through elementary functions:
The best-known properties and formulas of the Fibonacci and Lucas numbers
Simple values at zero and infinity
The Fibonacci and Lucas numbers 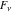 and and 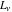 have the following values at zero and infinity: have the following values at zero and infinity:
Specific values for specialized variables
The Fibonacci and Lucas numbers 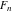 and and 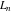 with integer argument with integer argument 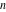 can be represented by the following formulas: can be represented by the following formulas:
For the cases of integer arguments 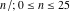 , the values of the Fibonacci and Lucas numbers , the values of the Fibonacci and Lucas numbers 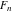 and and 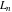 can be described by the following table: can be described by the following table:
Analyticity
The Fibonacci and Lucas numbers 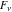 and and 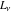 are entire analytical functions of are entire analytical functions of 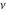 that are defined over the whole complex that are defined over the whole complex 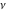 -plane: -plane:
Periodicity
The Fibonacci and Lucas numbers 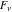 and and 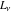 do not have periodicity. do not have periodicity.
Parity and symmetry
The Fibonacci and Lucas numbers 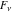 and and  generically do not have parity, but they have mirror symmetry: generically do not have parity, but they have mirror symmetry:
Poles and essential singularities
The Fibonacci and Lucas numbers 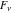 and and 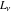 have only the singular point have only the singular point  . It is an essential singular point. . It is an essential singular point.
Branch points and branch cuts
The Fibonacci and Lucas numbers 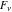 and and 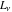 do not have branch points and branch cuts over the complex do not have branch points and branch cuts over the complex 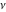 -plane. -plane.
Series representations
The Fibonacci and Lucas numbers 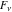 and and  have the following series expansions (which converge in the whole complex have the following series expansions (which converge in the whole complex 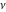 -plane): -plane):
Asymptotic series expansions
The asymptotic behavior of the Fibonacci and Lucas numbers 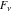 and and  is described by the following formulas: is described by the following formulas:
Other series representations
The Fibonacci and Lucas numbers 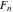 and and 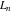 for integer nonnegative for integer nonnegative 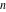 can be represented through the following sums involving binomials: can be represented through the following sums involving binomials:
Integral representations
The Fibonacci and Lucas numbers  and and 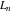 have the following integral representations on the real axis: have the following integral representations on the real axis:
Generating functions
The Fibonacci and Lucas numbers 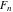 and and  can be represented as the coefficients of the series of the corresponding generating functions: can be represented as the coefficients of the series of the corresponding generating functions:
Transformations: Addition formulas
The Fibonacci and Lucas numbers 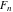 and and 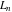 satisfy numerous addition formulas: satisfy numerous addition formulas:
Transformations: Multiple arguments
The Fibonacci and Lucas numbers 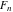 and and 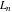 satisfy numerous identities, for example the following multiple argument formulas: satisfy numerous identities, for example the following multiple argument formulas:
Transformations: Products and powers of the direct function
The Fibonacci and Lucas numbers 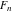 and and 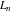 satisfy numerous identities for products and powers: satisfy numerous identities for products and powers:
Identities
The Fibonacci and Lucas numbers 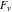 and and  are solutions of the following simple difference equation with constant coefficients: are solutions of the following simple difference equation with constant coefficients:
The Fibonacci and Lucas numbers  and and  satisfy numerous recurrence identities: satisfy numerous recurrence identities:
Other identities for Fibonacci and Lucas numbers 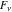 and and 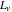 are just functional identities: are just functional identities:
Complex characteristics
The Fibonacci and Lucas numbers 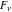 and and 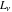 have the following complex characteristics for complex arguments: have the following complex characteristics for complex arguments:
Differentiation
The Fibonacci and Lucas numbers 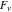 and and 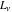 have the following representations for derivatives of the first and have the following representations for derivatives of the first and 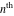 orders or the arbitrary fractional order orders or the arbitrary fractional order 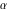 : :
Differential equations
The Fibonacci and Lucas numbers 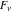 and and 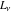 satisfy the following third-order linear differential equation: satisfy the following third-order linear differential equation:
where  , , 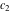 , and , and 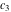 are arbitrary constants. are arbitrary constants.
Indefinite integration
Some indefinite integrals for Fibonacci and Lucas numbers 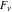 and and 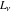 can be evaluated as follows: can be evaluated as follows:
Laplace transforms
Laplace transforms 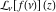 of the Fibonacci and Lucas numbers of the Fibonacci and Lucas numbers 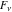 and and 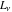 can be represented by the following formulas: can be represented by the following formulas:
Summation
There exist many formulas for finite summation of Fibonacci and Lucas numbers, for example:
Here are some corresponding infinite sums:
And here are some multiple sums:
Limit operation
Some formulas including limit operations with Fibonacci and Lucas numbers 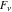 and and 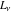 take on symmetrical forms: take on symmetrical forms:
Other identities
The Fibonacci numbers 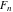 can be obtained from the evaluation of some determinates, for example: can be obtained from the evaluation of some determinates, for example:
Applications of the Fibonacci and Lucas numbers
Fibonacci and Lucas numbers have numerous applications throughout algebraic coding theory, linear sequential circuits, quasicrystals, phyllotaxies, biomathematics, and computer science.
|