|
Introduction to the rounding and congruence functions
General
The rounding and congruence functions have a long history that is closely related to the history of number theory. Many calculations use rounding of the floating-point and rational numbers to the closest smaller or larger integers. J. Nemorarius (1237) was one of the first mathematicians to use the quotient of two numbers 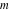 and and 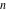 in a modern sense, but the word quotient appeared for the first time around 1250 in the writings of Meister Gernadus. in a modern sense, but the word quotient appeared for the first time around 1250 in the writings of Meister Gernadus.
Special notations for rounding and congruence functions were introduced much later. C. F. Gauss (1801) suggested the symbol mod (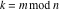 ) for the notation of the property that the ratio ) for the notation of the property that the ratio 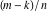 is an integer. He observed that is an integer. He observed that 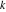 and and 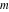 are the congruent modulo are the congruent modulo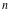 . The number . The number  is called modulus. is called modulus.
C. F. Gauss (1808) and J. Liouville (1838) widely used the floor and round functions in their investigations. They and other mathematicians used different and sometimes confusing notations for those functions. The modern notations of 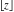 and and  for floor and ceiling functions, respectively, were suggested by K. E. Iverson (1962). The notation for floor and ceiling functions, respectively, were suggested by K. E. Iverson (1962). The notation 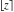 for the rounding function was proposed by J. Hastad (1988). for the rounding function was proposed by J. Hastad (1988).
Definitions of the rounding and congruence functions
The rounding and congruence functions include seven basic functions. They all deal with the separation of integer or fractional parts from real and complex numbers: the floor function (entire part function) 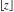 , the nearest integer function (round) , the nearest integer function (round) 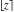 , the ceiling function (least integer) , the ceiling function (least integer) 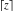 , the integer part , the integer part 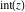 , the fractional part , the fractional part  , the modulo function (congruence) , the modulo function (congruence) 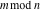 , and the integer part of the quotient (quotient or integer division) , and the integer part of the quotient (quotient or integer division) 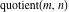 . .
The floor function (entire function)  can be considered as the basic function of this group. The other six functions can be uniquely defined through the floor function. can be considered as the basic function of this group. The other six functions can be uniquely defined through the floor function.
Floor
For real 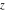 , the floor function , the floor function 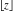 is the greatest integer less than or equal to is the greatest integer less than or equal to 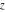 . .
For arbitrary complex 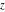 , the function , the function 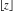 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples: 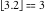 , , 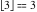 , , 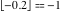 , , 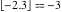 , , 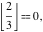 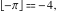  , , 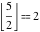 , ,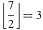 . .
Round
For real 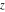 , the rounding function , the rounding function 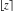 is the integer closest to is the integer closest to 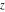 (if (if 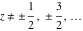 ). ).
For arbitrary 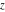 , the round function , the round function 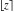 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples:  , , 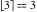 , , 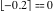 , , 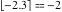 , , 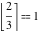 , , 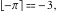 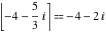 , , 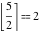 , , 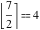 . .
Ceiling
For real 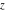 , the ceiling function , the ceiling function 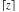 is the smallest integer greater than or equal to is the smallest integer greater than or equal to 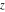 . .
For arbitrary 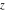 , the function , the function 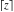 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples: 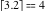 , , 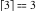 , , 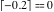 , , 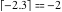 , ,  , , 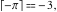 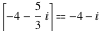 , , 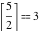 , , 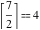 . .
Integer part
For real 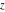 , the function integer part , the function integer part 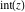 is the integer part of is the integer part of 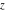 . .
For arbitrary 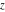 , the function , the function 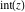 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples: 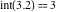 , , 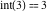 , ,  , , 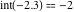 , , 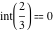 , , 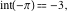 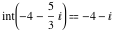 , , 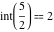 , ,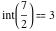 . .
Fractional part
For real 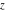 , the function fractional part , the function fractional part 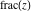 is the fractional part of is the fractional part of  . .
For arbitrary 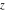 , the function , the function 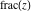 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples:  , , 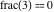 , , 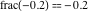 , , 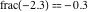 , , 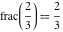 , ,  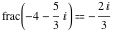 , , 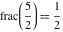 , , . .
Mod
For complex 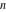 and and 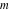 , the mod function , the mod function 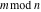 is the remainder of the division of is the remainder of the division of 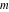 by by 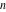 . The sign of . The sign of 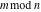 for real for real 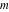 , , 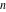 is always the same as the sign of is always the same as the sign of 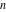 . .
The mod function 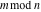 can be described (or defined) by the following formula: can be described (or defined) by the following formula:
The functional property 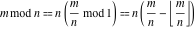 makes the behavior of makes the behavior of  similar to the behavior of similar to the behavior of 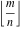 . .
Examples: 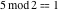 , , 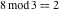 , , 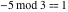 , , 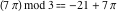 , , 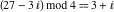 , ,  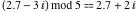 . .
Quotient
For complex 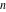 and and 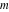 , the integer part of the quotient (quotient) function , the integer part of the quotient (quotient) function 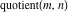 is the integer quotient of is the integer quotient of  and and 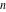 . .
The quotient function 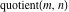 can be described (or defined) by the following formula: can be described (or defined) by the following formula:
Examples: 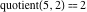 , , 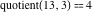 , , 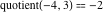 , , 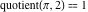 , , 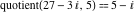 , , 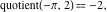 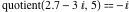 . .
Connections within the group of rounding and congruence functions and with other function groups
Representations through related functions
The rounding and congruence functions 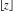 , , 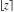 , , 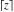 , , 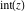 , , 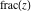 , , 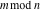 , and , and 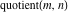 have numerous representations through related functions, which are shown in the following tables, where the symbol have numerous representations through related functions, which are shown in the following tables, where the symbol  means the characteristic function of a set means the characteristic function of a set 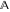 (having the value 1 when its argument (having the value 1 when its argument  is an element of the specified set 𝔸, and a value of 0 otherwise): is an element of the specified set 𝔸, and a value of 0 otherwise):
The rounding and congruence functions 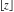 , , 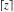 , , 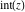 , , 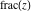 , , 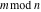 , and , and 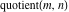 can also be represented through elementary functions by the following formulas: can also be represented through elementary functions by the following formulas:
The best-known properties and formulas of the number theory functions
Simple values at zero
The rounding and congruence functions  , ,  , ,  , , 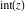 , and , and  have zero values at zero: have zero values at zero:
Specific values for specialized variables
The values of five rounding and congruence functions 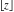 , , 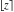 , , 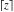 , , 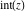 , and , and  at some fixed points or for specialized variables and infinities are shown in the following table: at some fixed points or for specialized variables and infinities are shown in the following table:
The values of mod function 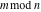 , and , and 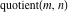 at some fixed points or for specialized variables are shown here: at some fixed points or for specialized variables are shown here:
Analyticity
All seven rounding and congruence functions (floor function 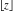 , round function , round function 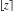 , ceiling function , ceiling function 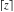 , integer part , integer part 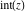 , fractional part , fractional part 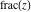 , mod function , mod function 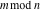 , and the quotient function , and the quotient function 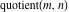 ) are not analytical functions. They are defined for all complex values of their arguments ) are not analytical functions. They are defined for all complex values of their arguments 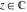 and and 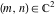 . The functions . The functions  , , 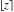 , , 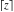 , and , and 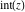 are piecewise constant functions and the functions are piecewise constant functions and the functions 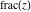 , , 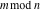 , and , and 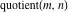 are piecewise continuous functions. are piecewise continuous functions.
Periodicity
The rounding and congruence functions 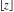 , ,  , , 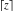 , ,  , , 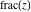 , and , and 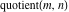 are not periodic functions. are not periodic functions.
 is a periodic function with respect to is a periodic function with respect to 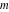 with period with period 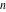 : :
Parity and symmetry
Four rounding and congruence functions (round function 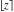 , integer part , integer part  , fractional part , fractional part  , and mod function , and mod function  ) are odd functions. The quotient function ) are odd functions. The quotient function 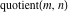 is an even function: is an even function:
The rounding and congruence functions 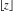 , , 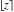 , , 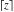 , , 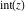 , and , and 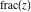 have the following mirror symmetry: have the following mirror symmetry:
Sets of discontinuity
The floor and ceiling functions 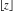 and and 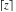 are piecewise constant functions with unit jumps on the lines are piecewise constant functions with unit jumps on the lines 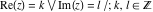 .
The functions .
The functions 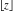 (and (and 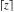 ) are continuous from the right (from the left) on the intervals ) are continuous from the right (from the left) on the intervals 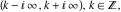 and from above (from below) on the intervals and from above (from below) on the intervals 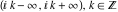 . .
The function 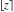 is a piecewise constant function with unit jumps on the lines is a piecewise constant function with unit jumps on the lines 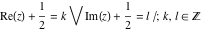 .
The function .
The function 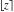 is continuous from the right on the intervals is continuous from the right on the intervals 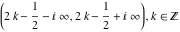 , and from the left on the intervals , and from the left on the intervals 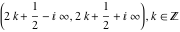 .
The function .
The function 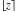 is continuous from above on the intervals is continuous from above on the intervals 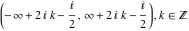 , and from below on the intervals , and from below on the intervals 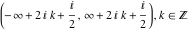 . .
The function  (and (and 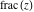 ) is a piecewise constant (continuous) function with unit jumps on the lines ) is a piecewise constant (continuous) function with unit jumps on the lines 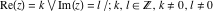 .
The functions .
The functions 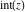 and and 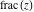 are continuous from the right on the intervals are continuous from the right on the intervals 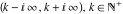 , and from the left on the intervals , and from the left on the intervals 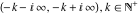 .
The functions .
The functions 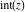 and and 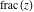 are continuous from above on the intervals are continuous from above on the intervals 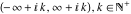 , and from below on the intervals , and from below on the intervals 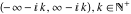 . .
The functions 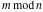 and and 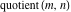 are piecewise continuous functions with jumps on the curves are piecewise continuous functions with jumps on the curves 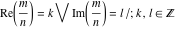 . The functional properties . The functional properties 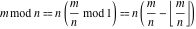 and and  make the behavior of that functions similar to the behavior of floor function make the behavior of that functions similar to the behavior of floor function 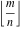 . .
The previous described properties can be described in more detail by the formulas from the following table:
Series representations
The rounding and congruence functions 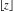 , , 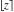 , , 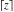 , ,  , , 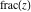 , , 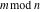 , and , and 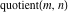 have the following series representations: have the following series representations:
Transformations and argument simplifications (arguments involving basic arithmetic operations)
The values of rounding and congruence functions 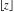 , , 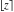 , , 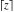 , , 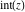 , and , and 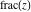 at the points at the points 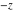 , , 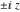 , , 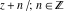 can also be represented by the following formulas: can also be represented by the following formulas:
The values of the functions 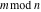 and and 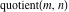 at the points at the points 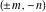 , , 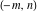 , , 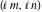 , , 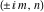 , , 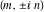 , and , and 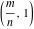 have the following representations: have the following representations:
Transformations and argument simplifications (arguments involving related functions)
Compositions of rounding and congruence functions 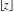 , , 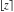 , ,  , , 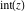 , , 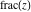 , , 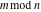 , and , and  with the rounding and congruence functions in many cases lead to very simple zero results: with the rounding and congruence functions in many cases lead to very simple zero results:
Addition formulas
The rounding and congruence functions 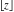 , ,  , , 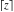 , , 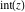 , and , and 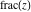 satisfy the following addition formulas: satisfy the following addition formulas:
Multiple arguments
The rounding and congruence functions 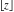 , , 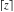 , , 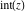 , , 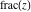 , , 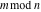 , and , and 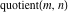 have the following relations for multiple arguments: have the following relations for multiple arguments:
Sums of the direct function
Sums of the floor and ceiling functions 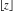 and and 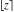 satisfy the following relations: satisfy the following relations:
Identities
All rounding and congruence functions satisfy numerous identities, for example:
Complex characteristics
Complex characteristics (real and imaginary parts 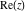 and and 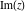 , absolute value , absolute value  , argument , argument 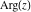 , complex conjugate , complex conjugate 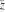 , and signum , and signum 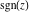 ) of the rounding and congruence functions can be represented in the forms shown in the following tables: ) of the rounding and congruence functions can be represented in the forms shown in the following tables:
Differentiation
Derivatives of the rounding and congruence functions  , , 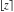 , , 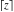 , , 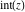 , , 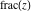 , , 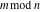 , and , and 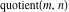 can be evaluated in the classical and distributional sense. In the last case, all variables should be real and results include the Dirac delta function. All rounding and congruence functions also have fractional derivatives. All these derivatives can be represented as shown in the following tables: can be evaluated in the classical and distributional sense. In the last case, all variables should be real and results include the Dirac delta function. All rounding and congruence functions also have fractional derivatives. All these derivatives can be represented as shown in the following tables:
Indefinite integration
Simple indefinite integrals of the rounding and congruence functions 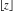 , ,  , , 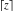 , , 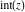 , , 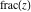 , , 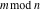 , and , and  have the following representations: have the following representations:
Definite integration
Some definite integrals of the rounding and congruence functions 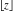 , ,  , , 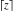 , , 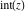 , , 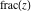 , , 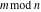 , and , and 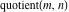 can be evaluated and are shown in the following table: can be evaluated and are shown in the following table:
Integral transforms
All Fourier transforms of the rounding and congruence functions  , , 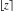 , , 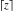 , , 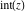 , , 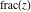 , ,  , and , and 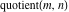 can be evaluated in a distributional sense and include the Dirac delta function: can be evaluated in a distributional sense and include the Dirac delta function:
Laplace and Mellin integral transforms of the rounding and congruence functions  , , 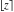 , , 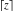 , , 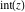 , ,  , ,  , and , and 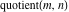 can be evaluated in the classical sense: can be evaluated in the classical sense:
Summation
Sometimes finite and infinite sums including rounding and congruence functions have rather simple representations, for example:
Zeros
Zeros of rounding and congruence functions are given as follows:
Applications of the rounding and congruence functions
All rounding and congruence functions are used throughout mathematics, the exact sciences, and engineering.
|