|
The Bessel functions have been known since the 18th century when mathematicians and scientists started to describe physical processes through differential equations. Many different‐looking processes satisfy the same partial differential equations. These equations were named Laplace, d`Alembert (wave), Poisson, Helmholtz, and heat (diffusion) equations. Different methods were used to investigate these equations. The most powerful was the separation of variables method, which in polar coordinates often leads to ordinary differential equations of special structure:
This equation with concrete values of the parameter 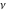 appeared in the articles by F. W. Bessel (1816, 1824) who built two partial solutions appeared in the articles by F. W. Bessel (1816, 1824) who built two partial solutions 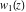 and and 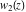 of the previous equation in the form of series: of the previous equation in the form of series:
Substituting the series into the differential equation produces the following solutions:
O. Schlömilch (1857) used the name Bessel functions for these solutions, E. Lommel (1868) considered 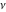 as an arbitrary real parameter, and H. Hankel (1869) considered complex values for as an arbitrary real parameter, and H. Hankel (1869) considered complex values for  . The two independent solutions of the differential equation were notated as . The two independent solutions of the differential equation were notated as 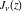 and and 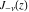 . .
For integer index  , the functions , the functions 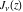 and and 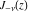 coincide or have different signs. In such cases, the second linear independent solution of the previous differential equation was introduced by C. G. Neumann (1867) as the limit case of the following special linear combination of the functions coincide or have different signs. In such cases, the second linear independent solution of the previous differential equation was introduced by C. G. Neumann (1867) as the limit case of the following special linear combination of the functions 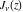 and and 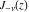 : :
J. Watson (1867) introduced the notation 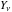 for this function. Other authors (H. Hankel (1869), H. Weber (1873), and L. Schläfli (1875)) investigated its properties. In particular, the general solution of the previous differential equation for all values of the parameter for this function. Other authors (H. Hankel (1869), H. Weber (1873), and L. Schläfli (1875)) investigated its properties. In particular, the general solution of the previous differential equation for all values of the parameter 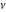 can be presented by the formula: can be presented by the formula:
where 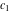 and and 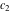 are arbitrary complex constants. are arbitrary complex constants.
In a similar way, A. B. Basset (1888) and H. M. MacDonald (1899) introduced the modified Bessel functions 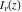 and and 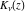 , which satisfy the modified Bessel differential equation: , which satisfy the modified Bessel differential equation:
The first differential equation can be converted into the last one by changing the independent variable 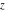 to to 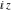 . .
|