|
Defining the hyperbolic cotangent function
The hyperbolic cotangent function is an old mathematical function. It was first used in the articles by L'Abbe Sauri (1774).
This function is easily defined as the ratio of the hyperbolic sine and cosine functions (or expanded, as the ratio of the half‐sum and half‐difference of two exponential functions in the points 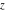 and and 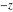 ): ):
This function can also be defined as reciprocal to the hyperbolic tangent function:
After comparison with the famous Euler formulas for the cosine and sine functions,  and and 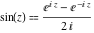 , it is easy to derive the following representation of the hyperbolic cotangent through the circular cotangent: , it is easy to derive the following representation of the hyperbolic cotangent through the circular cotangent:
This formula allows for the derivation of all properties and formulas for the hyperbolic cotangent from the corresponding properties and formulas for circular cotangent function.
|