|
Definition of the hyperbolic cotangent for a complex argument In the complex 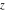 ‐plane, the function ‐plane, the function 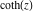 is defined by the same formula as for real values. is defined by the same formula as for real values. In the points 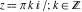 , where , where 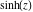 has zeros, the denominator of the last formula equals zero and has zeros, the denominator of the last formula equals zero and 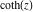 has singularities (poles of the first order). has singularities (poles of the first order). Here are two graphics showing the real and imaginary parts of the hyperbolic cotangent function over the complex plane:
|