|
The best-known properties and formulas for trigonometric functions
Real values for real arguments
For real values of argument 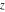 , the values of all the trigonometric functions are real (or infinity). , the values of all the trigonometric functions are real (or infinity).
In the points 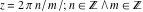 , the values of trigonometric functions are algebraic. In several cases they can even be rational numbers or integers (like , the values of trigonometric functions are algebraic. In several cases they can even be rational numbers or integers (like  or or  ). The values of trigonometric functions can be expressed using only square roots if ). The values of trigonometric functions can be expressed using only square roots if  and and  is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}. is a product of a power of 2 and distinct Fermat primes {3, 5, 17, 257, …}.
Simple values at zero
All trigonometric functions have rather simple values for arguments 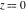 and and  : :
Analyticity
All trigonometric functions are defined for all complex values of  , and they are analytical functions of , and they are analytical functions of  over the whole complex over the whole complex  ‐plane and do not have branch cuts or branch points. The two functions ‐plane and do not have branch cuts or branch points. The two functions  and and  are entire functions with an essential singular point at are entire functions with an essential singular point at 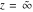 . All other trigonometric functions are meromorphic functions with simple poles at points . All other trigonometric functions are meromorphic functions with simple poles at points  for for  and and  , and at points , and at points  for for  and and  . .
Periodicity
All trigonometric functions are periodic functions with a real period ( or or  ): ):
Parity and symmetry
All trigonometric functions have parity (either odd or even) and mirror symmetry:
Simple representations of derivatives
The derivatives of all trigonometric functions have simple representations that can be expressed through other trigonometric functions:
Simple differential equations
The solutions of the simplest second‐order linear ordinary differential equation with constant coefficients can be represented through  and and  : :
All six trigonometric functions satisfy first-order nonlinear differential equations:
|