|
Riemann Surfaces Riemann surfaces of (zeta;zetak-z)j-1 The functions 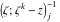 , , 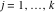 for for 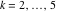 over the over the 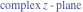 . The left graphic shows . The left graphic shows  and the right graphic shows and the right graphic shows 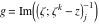 . The . The 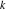 roots roots 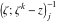 , , 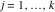 form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial 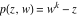 . The point . The point 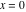 is the unique branch point of these functions. is the unique branch point of these functions. Riemann surfaces of (zeta;zetak-zk)j-1 The functions  , ,  for for 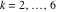 over the over the 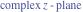 . The left graphic shows . The left graphic shows 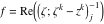 and the right graphic shows and the right graphic shows 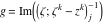 . The . The 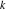 roots roots 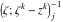 , , 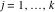 form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial 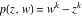 . It is split into . It is split into 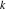 independent sheets. independent sheets. Riemann surfaces of (zeta;zetak-zk+1)j-1 The functions 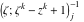 , , 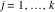 for for 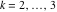 over the over the 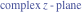 . The left graphic shows . The left graphic shows 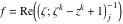 and the right graphic shows and the right graphic shows 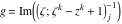 . The . The 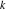 roots roots 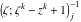 , , 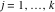 form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial 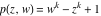 . The branch points are the roots of unity. . The branch points are the roots of unity. Riemann surfaces of (zeta;zetak-zeta-z)j-1 The functions 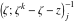 , ,  for for  over the over the 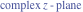 . The left graphic shows . The left graphic shows 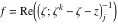 and the right graphic shows and the right graphic shows 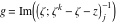 . The . The 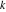 roots roots 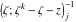 , , 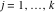 form the Riemann surface of the bivariate trinomial polynomial form the Riemann surface of the bivariate trinomial polynomial 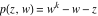 . . Riemann surfaces of (zeta;zetak-Summ=0kzm)j-1 The functions 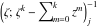 , , 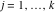 for for  over the over the 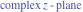 . The left graphic shows . The left graphic shows 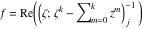 and the right graphic shows and the right graphic shows 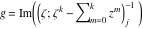 . The . The 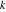 roots roots 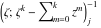 , , 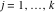 form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial  . . Riemann surfaces of (zeta;Summ=0kzetam-Summ=0kzm)j-1 The functions 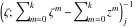 , , 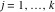 for for 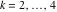 over the over the  . The left graphic shows . The left graphic shows 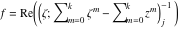 and the right graphic shows and the right graphic shows 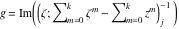 . The . The  roots roots 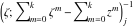 , , 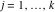 form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial 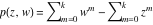 . . Riemann surfaces of (zeta;Summ=0kzetam-1/Summ=0kzm)j-1 The functions 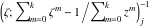 , , 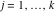 for for 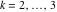 over the over the 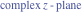 . The left graphic shows . The left graphic shows 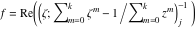 and the right graphic shows and the right graphic shows 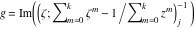 . The . The  roots roots 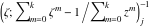 , ,  form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial 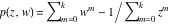 . . Riemann surfaces of (zeta;Summ=0kzetam Summ=0kzm)j-1 The functions  , , 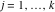 for for 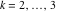 over the over the 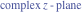 . The left graphic shows . The left graphic shows 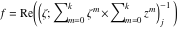 and the right graphic shows and the right graphic shows 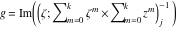 . The . The 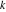 roots roots 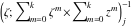 , ,  form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial 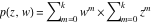 . . Riemann surfaces of various roots The functions 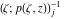 , , 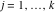 for various for various 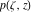 over the over the 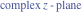 . The left graphic shows . The left graphic shows 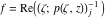 and the right graphic shows and the right graphic shows 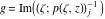 . The . The 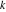 roots roots  , , 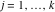 form the Riemann surface of the bivariate polynomial form the Riemann surface of the bivariate polynomial  . .
|