|
Tetraview animations The above graphics of the real part and imaginary part over the 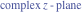 can be viewed as a projection of the surface in a four‐dimensional space with coordinates can be viewed as a projection of the surface in a four‐dimensional space with coordinates 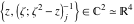 . This tetraview animation shows projections from the rotating four‐dimensional hypersurface . This tetraview animation shows projections from the rotating four‐dimensional hypersurface 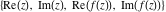 with with 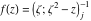 , , 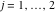 . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. The above graphics of the real part and imaginary part over the 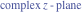 can be viewed as a projection of the surface in a four‐dimensional space with coordinates can be viewed as a projection of the surface in a four‐dimensional space with coordinates 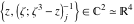 . This tetraview animation shows projections from the rotating four‐dimensional hypersurface . This tetraview animation shows projections from the rotating four‐dimensional hypersurface 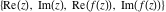 with with 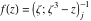 , , 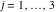 . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. The above graphics of the real part and imaginary part over the 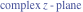 can be viewed as a projection of the surface in a four‐dimensional space with coordinates can be viewed as a projection of the surface in a four‐dimensional space with coordinates 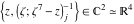 . This tetraview animation shows projections from the rotating four‐dimensional hypersurface . This tetraview animation shows projections from the rotating four‐dimensional hypersurface 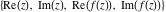 with with 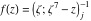 , , 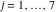 . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. The above graphics of the real part and imaginary part over the 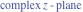 can be viewed as a projection of the surface in a four‐dimensional space with coordinates can be viewed as a projection of the surface in a four‐dimensional space with coordinates 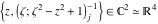 . This tetraview animation shows projections from the rotating four‐dimensional hypersurface . This tetraview animation shows projections from the rotating four‐dimensional hypersurface 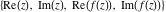 with with 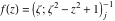 , , 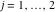 . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. The above graphics of the real part and imaginary part over the 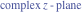 can be viewed as a projection of the surface in a four‐dimensional space with coordinates can be viewed as a projection of the surface in a four‐dimensional space with coordinates 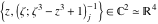 . This tetraview animation shows projections from the rotating four‐dimensional hypersurface . This tetraview animation shows projections from the rotating four‐dimensional hypersurface 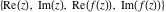 with with 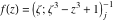 , , 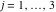 . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension. . The right legend indicates the current orientation of the hypersurface in 4D. The coloring is according to the value of the fourth dimension.
|