|
Calculating the series expansion of a secant function to hundreds of terms can be done in seconds. Mathematica comes with the add‐on package DiscreteMath`RSolve` that allows finding the general terms of series for many functions. After loading this package, and using the package function SeriesTerm, the following 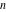 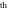 term of term of 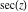 can be evaluated. can be evaluated. Here is a quick check of the last result. This series should be evaluated to 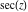 , which can be concluded from the following relation. , which can be concluded from the following relation. Mathematica can evaluate derivatives of the secant function of an arbitrary positive integer order. Mathematica can calculate some finite symbolic products that contain the secant function. Here are two examples. Mathematica can calculate a huge number of doable indefinite integrals that contain the secant function. The results can contain special functions. Here are some examples. Mathematica can calculate wide classes of definite integrals that contain the secant function. Here are some examples. Mathematica can calculate limits that contain the secant function. Here are some examples. The next inputs solve two equations that contain the secant function. Because of the multivalued nature of the inverse secant function, a printed message indicates that only some of the possible solutions are returned. A complete solution of the previous equation can be obtained using the function Reduce. Here is a nonlinear first-order differential equation that is obeyed by the secant function. Mathematica can find the general solution of this differential equation. In doing so, the generically multivariate inverse of a function is encountered, and a message is issued that a solution branch is potentially missed. Mathematica has built‐in functions for 2D and 3D graphics. Here are some examples.
|