|
Representation through more general functions
The hyperbolic secant function 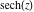 can be represented using more general mathematical functions. As the reciprocal to the hyperbolic cosine function that is a particular case of the generalized hypergeometric, Bessel, Struve, and Mathieu functions, the hyperbolic secant function can also be represented as reciprocal to those special functions. Here are some examples: can be represented using more general mathematical functions. As the reciprocal to the hyperbolic cosine function that is a particular case of the generalized hypergeometric, Bessel, Struve, and Mathieu functions, the hyperbolic secant function can also be represented as reciprocal to those special functions. Here are some examples:
But these representations are not very useful because they include complicated special functions in the denominators.
It is more useful to write the secant function as particular cases of one special function. That can be done using doubly periodic Jacobi elliptic functions that degenerate into the hyperbolic secant function when their second parameter is equal to 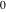 or or 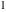 : :
|