|
In the complex 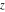 ‐plane, the function ‐plane, the function 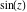 is defined using the exponential function is defined using the exponential function  in the points in the points 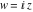 and and 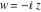 through the formula: through the formula: The key role in this definition of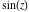 belongs to the famous Euler formula connecting the exponential, the sine, and the cosine functions: belongs to the famous Euler formula connecting the exponential, the sine, and the cosine functions: Changing 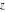 to to 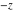 , the Euler formula becomes: , the Euler formula becomes: Taking the difference of the preceding formulas and dividing by 2ⅈ gives the following result: Here are two graphics showing the real and imaginary parts of the sine function over the complex plane.
|