|
Entering the complex plane 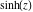 in the upper half of the in the upper half of the  near the real axis viewed from the lower half‐plane.
Here the complex variable near the real axis viewed from the lower half‐plane.
Here the complex variable 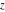 is expressed as is expressed as 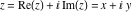 . The red surface is the real part of . The red surface is the real part of 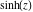 . The blue, semitransparent surface is the imaginary part of . The blue, semitransparent surface is the imaginary part of 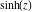 . The pink tube is the real part of the function . The pink tube is the real part of the function 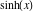 along the real axis and the skyblue tube is the imaginary part of the function along the real axis and the skyblue tube is the imaginary part of the function 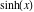 along the real axis. Along the real axis, the real part is a monotonic function that is exponentially increasing; going away from the real axis into the along the real axis. Along the real axis, the real part is a monotonic function that is exponentially increasing; going away from the real axis into the 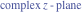 gives an oscillating function. The imaginary part vanishes identically along the real axis. gives an oscillating function. The imaginary part vanishes identically along the real axis.
Real part over the complex plane The real part of 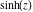 where where 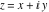 . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the real part of . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the real part of 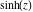 is a monotonic function; going away from the real axis into the is a monotonic function; going away from the real axis into the 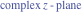 gives an oscillating function. gives an oscillating function. The absolute value of the real part of 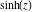 where where 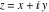 . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the absolute value of the real part of . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the absolute value of the real part of 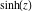 is exponentially increasing; going away from the real axis into the is exponentially increasing; going away from the real axis into the 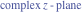 gives an oscillating function. gives an oscillating function. Imaginary part over the complex plane The imaginary part of 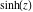 where where 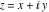 . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of 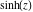 vanishes identically; going away from the real axis into the vanishes identically; going away from the real axis into the 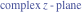 gives an oscillating function. gives an oscillating function. The absolute value of the imaginary part of 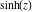 where where 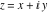 . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of 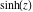 vanishes identically. vanishes identically. Absolute value part over the complex plane The absolute value of 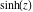 where where 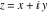 . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The zeros at . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The zeros at 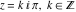 are visible. are visible. Argument over the complex plane The argument of 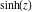 where where 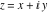 . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. 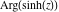 has lines of discontinuities over the has lines of discontinuities over the  . . The square of the sine of the argument of 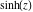 where where 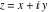 . For dominantly real values, the function values are near 0, and for dominantly imaginary values, the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclically colored contour plot of the argument. Red represents arguments near . For dominantly real values, the function values are near 0, and for dominantly imaginary values, the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclically colored contour plot of the argument. Red represents arguments near 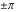 and light‐blue represents arguments near 0. and light‐blue represents arguments near 0. Zero-pole plot The logarithm of the absolute value of 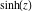 where where 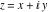 in the upper half‐plane. The surface is colored according to the square of the argument. In this plot, zeros are easily visible as spikes extending downwards a and poles and logarithmic singularities as spikes extending upwards. The zeros at in the upper half‐plane. The surface is colored according to the square of the argument. In this plot, zeros are easily visible as spikes extending downwards a and poles and logarithmic singularities as spikes extending upwards. The zeros at 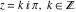 are visible. are visible. Real part over the complex plane near infinity The real part of 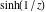 where where 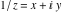 . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At 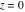 the function the function 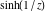 has an essential singularity. has an essential singularity. The absolute value of the real part of 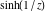 where where 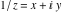 . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At 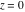 , the function , the function 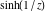 has an essential singularity. has an essential singularity. Imaginary part over the complex plane near infinity The imaginary part of 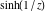 where where 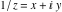 . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At 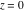 , the function , the function 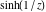 has an essential singularity. has an essential singularity. The absolute value of the imaginary part of 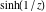 where where  . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At 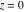 , the function , the function 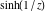 has an essential singularity. has an essential singularity. Absolute value part over the complex plane near infinity The absolute value of 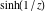 where where 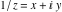 . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At 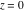 , the function , the function 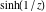 has an essential singularity. The two colored dots in the right graphic are the zeros at has an essential singularity. The two colored dots in the right graphic are the zeros at 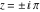 . . Argument over the complex plane near infinity The argument of 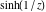 where where 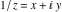 . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At 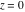 , the function , the function 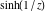 has an essential singularity. has an essential singularity. The square of the sine of the argument of 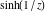 where where 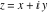 . For dominantly real values, the function values are near 0, and for dominantly imaginary values, the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclical colored contour plot of the argument. Red represents arguments near . For dominantly real values, the function values are near 0, and for dominantly imaginary values, the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclical colored contour plot of the argument. Red represents arguments near 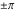 and light‐blue represents arguments near 0. and light‐blue represents arguments near 0. Zero-pole plot near infinity The logarithm of the absolute value of 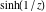 where where 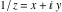 in the upper half‐plane. The surface is colored according to the square of the argument. In this plot, zeros are easily visible as spikes extending downwards and poles and logarithmic singularities as spikes extending upwards. At in the upper half‐plane. The surface is colored according to the square of the argument. In this plot, zeros are easily visible as spikes extending downwards and poles and logarithmic singularities as spikes extending upwards. At 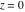 , the function , the function 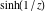 has an essential singularity. has an essential singularity.
|