|
Defining the tangent function
The tangent function is an old mathematical function. It was mentioned in 1583 by T. Fincke who introduced the word "tangens" in Latin. E. Gunter (1624) used the notation "tan", and J. H. Lambert (1770) discovered the continued fraction representation of this function.
The classical definition of the tangent function for real arguments is: "the tangent of an angle 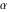 in a right‐angle triangle is the ratio of the length of the opposite leg to the length of the adjacent leg." This description of in a right‐angle triangle is the ratio of the length of the opposite leg to the length of the adjacent leg." This description of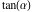 is valid for is valid for 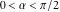 when the triangle is nondegenerate. This approach to the tangent can be expanded to arbitrary real values of when the triangle is nondegenerate. This approach to the tangent can be expanded to arbitrary real values of 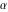 if consideration is given to the arbitrary point if consideration is given to the arbitrary point 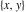 in the in the 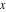 , ,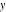 ‐Cartesian plane and ‐Cartesian plane and 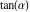 is defined as the ratio is defined as the ratio 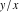 , assuming that α is the value of the angle between the positive direction of the , assuming that α is the value of the angle between the positive direction of the 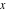 ‐axis and the direction from the origin to the point ‐axis and the direction from the origin to the point 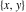 . .
Comparing this definition with definitions of the sine and cosine functions shows that the following formula can also be used as a definition of the tangent function:
|