|
The arithmetic‐geometric mean 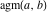 can be exactly evaluated in some points, for example: can be exactly evaluated in some points, for example:
For real values of arguments 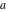 , , 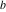 (with (with 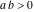 ), the values of the arithmetic‐geometric mean ), the values of the arithmetic‐geometric mean 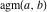 are real. are real.
The arithmetic‐geometric mean 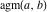 is an analytical function of is an analytical function of 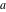 and and 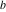 that is defined over that is defined over 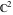 . .
The arithmetic‐geometric mean 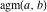 does not have poles and essential singularities. does not have poles and essential singularities.
The arithmetic‐geometric mean 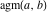 on the on the 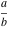 ‐plane has two branch points: ‐plane has two branch points: 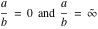 . It is a single‐valued function on the . It is a single‐valued function on the 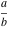 ‐plane cut along the interval ‐plane cut along the interval 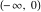 , where it is continuous from above: , where it is continuous from above:
The arithmetic‐geometric mean 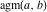 does not have periodicity. does not have periodicity.
The arithmetic‐geometric mean 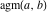 is an odd function and has mirror and permutation symmetry: is an odd function and has mirror and permutation symmetry:
The arithmetic‐geometric mean 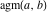 is the homogenous function: is the homogenous function:
The arithmetic‐geometric mean 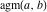 has the following series representations at the points has the following series representations at the points 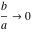 , , 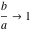 , and , and 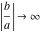 : :
The arithmetic‐geometric mean 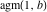 has the following infinite product representation: has the following infinite product representation:
The arithmetic‐geometric mean 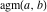 has the following integral representation: has the following integral representation:
The arithmetic‐geometric mean 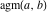 has the following limit representation, which is often used for the definition of has the following limit representation, which is often used for the definition of 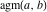 : :
The homogeneity property of the arithmetic‐geometric mean 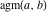 leads to the following transformations: leads to the following transformations:
Another group of transformations is based on the first of the following properties:
The first derivatives of the arithmetic‐geometric mean 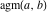 have rather simple representations: have rather simple representations:
The 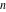 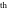 -order symbolic derivatives are much more complicated. Here is an example: -order symbolic derivatives are much more complicated. Here is an example:
The arithmetic‐geometric mean 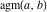 satisfies the following second-order ordinary nonlinear differential equation: satisfies the following second-order ordinary nonlinear differential equation:
It can also be represented as partial solutions of the following partial differential equation:
The arithmetic‐geometric mean 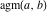 lies between the middle geometric mean and middle arithmetic mean, which is shown in the following famous inequality: lies between the middle geometric mean and middle arithmetic mean, which is shown in the following famous inequality:
|