|
For real values of the arguments 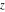 , , 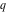 (with (with 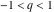 ), the values of the Jacobi theta functions ), the values of the Jacobi theta functions 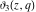 , , 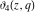 , , 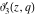 , and , and 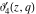 are real. are real.
For real values of the arguments 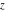 , , 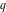 (with (with 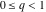 ), the values of the Jacobi theta functions ), the values of the Jacobi theta functions 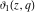 , , 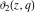 , , 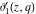 , and , and 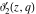 are real. are real.
All Jacobi theta functions 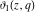 , , 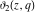 , , 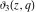 , , 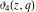 , , 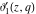 , , 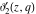 , , 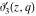 , and , and 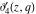 have the following simple values at the origin point: have the following simple values at the origin point:
All Jacobi theta functions 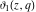 , , 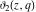 , , 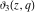 , , 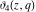 , , 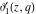 , , 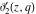 , , 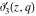 , and , and 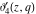 have the following simple values if have the following simple values if 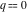 : :
At the points 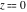 and and 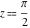 , all theta functions , all theta functions 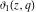 , , 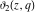 , , 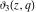 , , 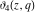 , , 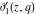 , , 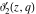 , , 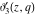 , and , and 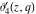 can be expressed through the Dedekind eta function can be expressed through the Dedekind eta function 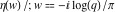 or a composition of the complete elliptic function or a composition of the complete elliptic function 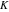 and the inverse elliptic nome and the inverse elliptic nome 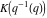 by the following formulas: by the following formulas:
The previous relations can be generalized for the cases 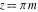 and and 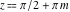 , where , where 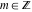 : :
All Jacobi theta functions 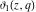 , , 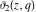 , , 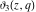 , , 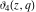 , , 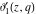 , , 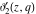 , , 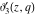 , and , and 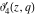 are analytic functions of are analytic functions of 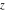 and and 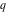 for for 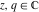 and and 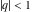 . .
All Jacobi theta functions 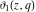 , , 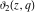 , , 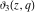 , , 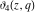 , , 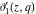 , , 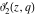 , , 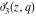 , and , and 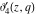 do not have poles and essential singularities inside of the unit circle do not have poles and essential singularities inside of the unit circle 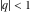 . .
For fixed 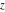 , the functions , the functions 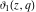 , , 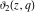 , , 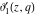 , and , and 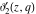 have one branch point: have one branch point: 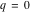 . (The point . (The point 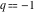 is the branch cut endpoint.) is the branch cut endpoint.)
For fixed 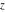 , the functions , the functions 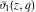 , , 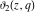 , , 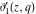 , and , and 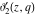 are the single‐valued functions inside the unit circle of the complex are the single‐valued functions inside the unit circle of the complex 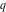 ‐plane, cut along the interval ‐plane, cut along the interval 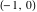 , where they are continuous from above: , where they are continuous from above:
For fixed 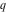 , the functions , the functions 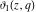 , , 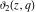 , , 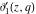 , and , and 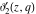 do not have branch points and branch cuts with respect to do not have branch points and branch cuts with respect to 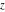 . .
The functions 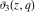 , , 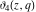 , , 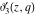 , and , and 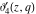 do not have branch points and branch cuts. do not have branch points and branch cuts.
The unit circle 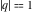 is the natural boundary of the region of analyticity for all Jacobi theta functions is the natural boundary of the region of analyticity for all Jacobi theta functions 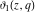 , , 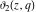 , , 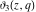 , , 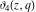 , , 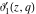 , , 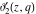 , , 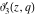 , and , and 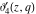 . .
The Jacobi theta functions 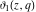 and and 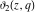 are the periodic functions with respect to are the periodic functions with respect to 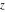 with period with period 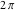 and a quasi‐period and a quasi‐period 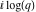 : :
The Jacobi theta functions 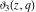 and and 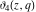 are the periodic functions with respect to are the periodic functions with respect to 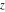 with period with period 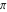 and a quasi‐period and a quasi‐period 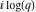 : :
The Jacobi theta functions 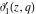 and and 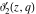 are the periodic functions with respect to are the periodic functions with respect to 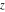 with period with period 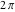 : :
The Jacobi theta functions 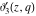 and and 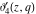 are the periodic functions with respect to are the periodic functions with respect to 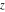 with period with period 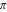 : :
The previous formulas are the particular cases of the following general relations that reflect the periodicity and quasi‐periodicity of the theta functions by variable  : :
All Jacobi theta functions 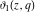 , , 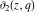 , , 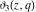 , , 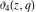 , , 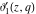 , , 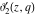 , , 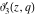 , and , and 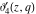 have mirror symmetry: have mirror symmetry:
The Jacobi theta functions 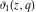 , , 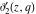 , , 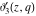 , and , and 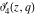 are odd functions with respect to are odd functions with respect to 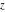 : :
The other Jacobi theta functions 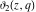 , , 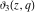 , , 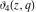 , and , and 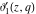 are even functions with respect to are even functions with respect to 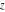 : :
The Jacobi theta functions 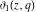 , , 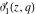 , , 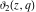 , and , and 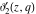 satisfy the following parity type relations with respect to satisfy the following parity type relations with respect to 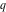 : :
The Jacobi theta functions 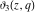 , , 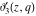 , , 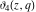 , and , and 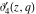 with argument with argument 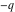 can be self-transformed by the following relations: can be self-transformed by the following relations:
All Jacobi elliptic theta functions 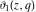 , , 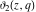 , , 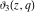 , and , and 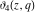 , and their derivatives , and their derivatives 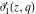 , , 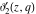 , , 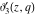 , and , and 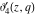 have the following series expansions, which can be called have the following series expansions, which can be called 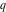 ‐series representations: ‐series representations:
The theta functions 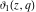 , , 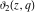 , , 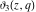 , and , and 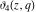 , and their derivatives , and their derivatives 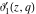 , , 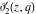 , , 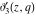 , and , and 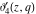 can also be represented through the following series: can also be represented through the following series:
The theta functions can be represented through infinite products, for example:
The theta functions 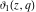 , , 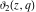 , , 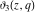 , and , and 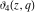 satisfy numerous relations that can provide transformations of their arguments, for example: satisfy numerous relations that can provide transformations of their arguments, for example:
Among those transformations, several kinds can be combined into specially named groups:
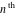 root of root of 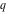 : :
Multiple angle formulas:
Double-angle formulas (which are not particular cases of the previous group), for example:
Landen's transformation:
The theta functions at 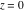 satisfy numerous modular identities of the form satisfy numerous modular identities of the form 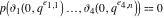 , where the , where the 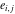 are positive integers and are positive integers and 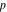 is a multivariate polynomials over the integers, for example: is a multivariate polynomials over the integers, for example:
Among the numerous identities for theta functions, several kinds can be joined into specially named groups:
Relations involving squares:
Relations involving quartic powers:
Relations between the four theta functions where the first argument is zero, for example:
Addition formulas:
Triple addition formulas, for example:
The derivatives of the Jacobi theta functions 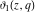 , , 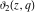 , , 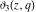 , and , and 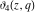 , and their derivatives , and their derivatives 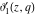 , , 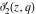 , , 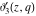 , and , and 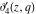 with respect to variable with respect to variable 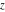 can be expressed by the following formulas: can be expressed by the following formulas:
The derivatives of the Jacobi theta functions 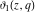 , , 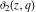 , , 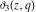 , and , and 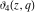 , and their derivatives , and their derivatives 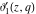 , , 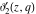 , , 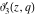 , and , and 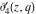 with respect to variable with respect to variable 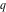 can be expressed by the following formulas: can be expressed by the following formulas:
The 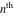 -order derivatives of the Jacobi theta functions -order derivatives of the Jacobi theta functions 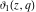 , , 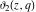 , , 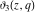 , and , and 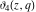 , and their derivatives , and their derivatives 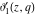 , , 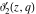 , , 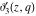 , and , and 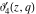 with respect to variable with respect to variable 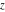 can be expressed by the following formulas: can be expressed by the following formulas:
The 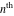 -order derivatives of Jacobi theta functions -order derivatives of Jacobi theta functions 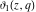 , , 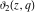 , , 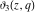 , and , and 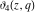 , and their derivatives , and their derivatives 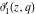 , , 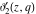 , , 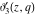 , and , and 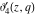 with respect to variable with respect to variable 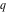 can be expressed by the following formulas: can be expressed by the following formulas:
The indefinite integrals of the Jacobi theta functions 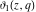 , , 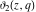 , , 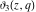 , and , and 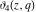 , and their derivatives , and their derivatives 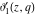 , , 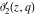 , , 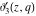 , and , and 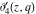 with respect to variable with respect to variable 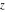 can be expressed by the following formulas: can be expressed by the following formulas:
The first four sums cannot be expressed in closed form through the named functions.
The indefinite integrals of the Jacobi theta functions 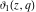 , , 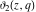 , , 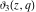 , and , and 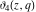 , and their derivatives , and their derivatives 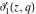 , , 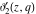 , , 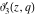 , and , and 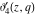 with respect to variable with respect to variable 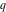 can be expressed by the following formulas: can be expressed by the following formulas:
The elliptic theta functions 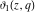 , , 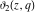 , , 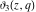 , and , and 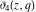 , and their derivatives , and their derivatives 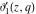 , , 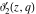 , , 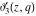 , and , and 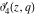 satisfy the one‐dimensional heat equations: satisfy the one‐dimensional heat equations:
The elliptic theta functions 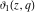 , , 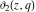 , , 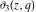 , and , and 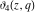 , and their derivatives , and their derivatives 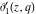 , , 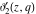 , , 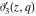 , and , and 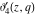 satisfy the following second-order partial differential equations: satisfy the following second-order partial differential equations:
The Jacobi theta functions 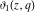 , , 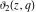 , , 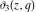 , and , and 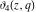 , and their derivatives , and their derivatives 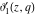 , , 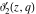 , , 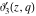 , and , and 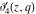 are equal to zero in the following points: are equal to zero in the following points:
|