|
The twelve Jacobi functions  , , 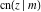 , , 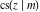 , , 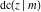 , , 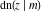 , , 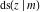 , , 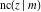 , , 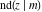 , ,  , ,  , , 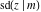 , and , and 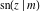 can be represented through the Weierstrass sigma functions: can be represented through the Weierstrass sigma functions:
The twelve Jacobi functions  , , 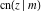 , , 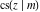 , , 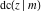 , , 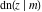 , , 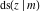 , , 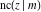 , , 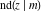 , , 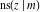 , , 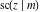 , , 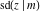 , and , and 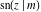 can be represented through the Weierstrass can be represented through the Weierstrass  function: function:
The twelve Jacobi functions 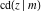 , , 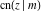 , , 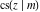 , , 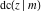 , ,  , , 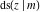 , , 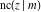 , ,  , , 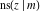 , , 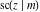 , ,  , and , and 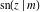 can be represented through the elliptic theta functions: can be represented through the elliptic theta functions:
The twelve Jacobi functions  , , 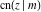 , , 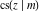 , , 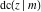 , , 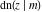 , , 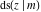 , , 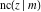 , , 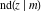 , , 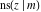 , , 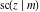 , , 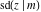 , and , and 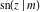 can be represented through the Neville theta functions: can be represented through the Neville theta functions:
The Jacobi functions 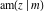 , , 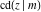 , , 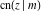 , , 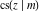 , , 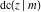 , ,  , ,  , , 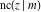 , , 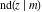 , , 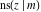 , , 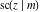 , ,  , and , and 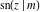 are connected with the corresponding inverse functions by the following formulas: are connected with the corresponding inverse functions by the following formulas:
By definition, the three basic Jacobi functions have the following representations through the amplitude function 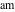 : :
The other nine Jacobi functions can be easily expressed through the three basic Jacobi functions 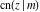 , , 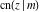 , and , and 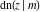 and, consequently, they can also be represented through the amplitude function and, consequently, they can also be represented through the amplitude function 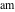 . .
The twelve Jacobi functions 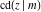 , , 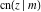 , , 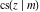 , , 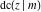 , , 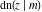 , , 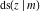 , , 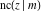 , ,  , , 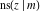 , , 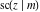 , , 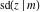 , and , and 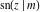 are interconnected by formulas that include rational functions, simple powers, and arithmetical operations from other Jacobi functions. These formulas can be divided into the following eleven groups: are interconnected by formulas that include rational functions, simple powers, and arithmetical operations from other Jacobi functions. These formulas can be divided into the following eleven groups:
Representations of 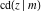 through other Jacobi functions are: through other Jacobi functions are:
Representations of 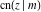 through other Jacobi functions are: through other Jacobi functions are:
Representations of 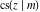 through other Jacobi functions are: through other Jacobi functions are:
Representations of 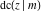 through other Jacobi functions are: through other Jacobi functions are:
Representations of 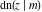 through other Jacobi functions are: through other Jacobi functions are:
Representations of  through other Jacobi functions are: through other Jacobi functions are:
Representations of 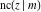 through other Jacobi functions are: through other Jacobi functions are:
Representations of 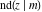 through other Jacobi functions are: through other Jacobi functions are:
Representations of  through other Jacobi functions are: through other Jacobi functions are:
Representations of 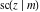 through other Jacobi functions are: through other Jacobi functions are:
Representations of 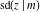 through other Jacobi functions are: through other Jacobi functions are:
Representations of 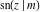 through other Jacobi functions are: through other Jacobi functions are:
|