|
The creation and development of the elliptic functions' theory in the 18th century required the introduction of special supporting utility functions, which were frequently used for description of the properties of the elliptic functions. Among such utilities the basic role is played by so-called Weierstrass invariants and Weierstrass half-periods. These were given the unusual notations 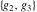 and { and {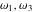 } instead of a consecutive numbering. The Weierstrass utility functions are a pair of bivariate functions that are inverses of each other: } instead of a consecutive numbering. The Weierstrass utility functions are a pair of bivariate functions that are inverses of each other:
Half-periods 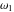 and and 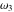 (and (and 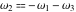 ) were mentioned in the works of C. G. J. Jacobi (1835), K. Weierstrass (1862), and A. Hurwitz (1905). The invariants ) were mentioned in the works of C. G. J. Jacobi (1835), K. Weierstrass (1862), and A. Hurwitz (1905). The invariants 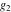 and and 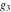 were mentioned in the works of A. Cayley and G. Boole (1845). were mentioned in the works of A. Cayley and G. Boole (1845).
Numerous formulas of Weierstrass elliptic functions include values of the Weierstrass 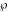 function and the Weierstrass zeta functions function and the Weierstrass zeta functions 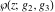 and and 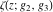 at the points at the points 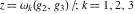 . These values have the following widely used notations: . These values have the following widely used notations:
|