|
Introduction to the Weierstrass functions and inverses
General
Historical remarks
The Weierstrass elliptic functions are identified with the famous mathematicians N. H. Abel (1827) and K. Weierstrass (1855, 1862). In the year 1849, C. Hermite first used the notation ℘123 for the basic Weierstrass doubly periodic function with only one double pole. The sigma and zeta Weierstrass functions were introduced in the works of F. G. Eisenstein (1847) and K. Weierstrass (1855, 1862, 1895).
The Weierstrass elliptic and related functions can be defined as inversions of elliptic integrals like 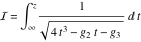 and and 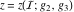 . Such integrals were investigated in the works of L. Euler (1761) and J.‐L. Lagrange (1769), who basically introduced the functions that are known today as the inverse Weierstrass functions. . Such integrals were investigated in the works of L. Euler (1761) and J.‐L. Lagrange (1769), who basically introduced the functions that are known today as the inverse Weierstrass functions.
Periodic functions
An analytic function 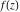 is called periodic if there exists a complex constant is called periodic if there exists a complex constant  such that such that  . The number . The number 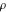 (with a minimal possible value of (with a minimal possible value of 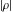 ) is called the period of the function ) is called the period of the function 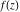 . .
Examples of well‐known singly periodic functions are the exponential functions, all the trigonometric and hyperbolic functions: 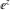 , sin(z), cos(z), csc(z), sec(z), tan(z), cot(z), sinh(z), cosh(z), csch(z), sech(z), tanh(z), and coth(z), which have periods , sin(z), cos(z), csc(z), sec(z), tan(z), cot(z), sinh(z), cosh(z), csch(z), sech(z), tanh(z), and coth(z), which have periods 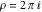 , , 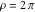 , , 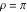 , , 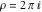 , and , and 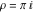 . The study of such functions can be restricted to any period‐strip . The study of such functions can be restricted to any period‐strip 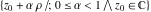 , because outside this strip, the values of these functions coincide with their corresponding values inside the strip. , because outside this strip, the values of these functions coincide with their corresponding values inside the strip.
Nonconstant analytic functions over the field of complex numbers cannot have more than two independent periods. So, generically, periodic functions can satisfy the following relations:
where 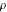 , , 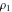 , and , and 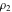 are periods (basic primitive periods). The condition are periods (basic primitive periods). The condition 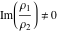 for doubly periodic functions implies the existence of a period‐parallelogram for doubly periodic functions implies the existence of a period‐parallelogram 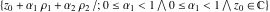 , which is the analog of the period‐strip , which is the analog of the period‐strip 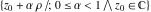 for singly periodic functions with period for singly periodic functions with period 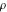 . .
In the case 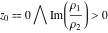 , this parallelogram is called the basic fundamental period‐parallelogram: , this parallelogram is called the basic fundamental period‐parallelogram: 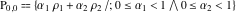 . The two line segments . The two line segments 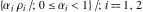 lying on the boundary of the period-parallelogram and beginning from the origin lying on the boundary of the period-parallelogram and beginning from the origin 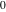 belong to belong to 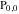 . The region . The region 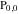 includes only one corner point includes only one corner point 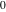 from four points lying at the boundary of the parallelogram with corners in from four points lying at the boundary of the parallelogram with corners in 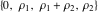 .
Sometimes the convention .
Sometimes the convention 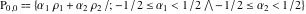 is used. is used.
The set of all such period‐parallelograms:
covers all complex planes: 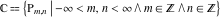 . .
Any doubly periodic function 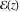 is called an elliptic function. The set of numbers is called an elliptic function. The set of numbers 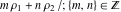 is called the period‐lattice for elliptic function is called the period‐lattice for elliptic function  . .
An elliptic function 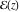 , which does not have poles in the period‐parallelogram, is equal to a constant (Liouville's theorem). , which does not have poles in the period‐parallelogram, is equal to a constant (Liouville's theorem).
Nonconstant elliptic (doubly periodic) functions 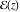 cannot be entire functions. This is not the case for singly periodic functions, for example, cannot be entire functions. This is not the case for singly periodic functions, for example, 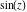 is entire function. is entire function.
Any nonconstant elliptic function 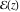 has at least two simple poles or at least one double pole in any period‐parallelogram. The sum of all its residues at the poles inside a period‐parallelogram is zero. has at least two simple poles or at least one double pole in any period‐parallelogram. The sum of all its residues at the poles inside a period‐parallelogram is zero.
The numbers of the zeros and poles of a nonconstant elliptic function 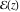 in a fundamental period‐parallelogram P are finite. in a fundamental period‐parallelogram P are finite.
The number of the zeros of 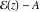 , where , where 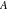 is any complex number, in a fundamental period‐parallelogram is any complex number, in a fundamental period‐parallelogram 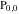 does not depend on the value does not depend on the value 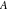 and coincides with number and coincides with number 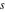 of the poles of the poles 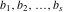 counted according to their multiplicity ( counted according to their multiplicity (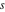 is called the order of the elliptic function is called the order of the elliptic function 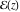 ). ).
The simplest elliptic function has order 2.
Let 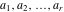 (and (and 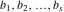 ) be the zeros (and poles) of a nonconstant elliptic function ) be the zeros (and poles) of a nonconstant elliptic function 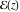 in a fundamental period‐parallelogram in a fundamental period‐parallelogram 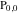 , both listed one or more times according to their multiplicity. Then the following hold: , both listed one or more times according to their multiplicity. Then the following hold:
So, the number of zeros of a nonconstant elliptic function 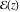 in the fundamental period‐parallelogram in the fundamental period‐parallelogram 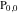 is equal to the number of poles there and counted according to their multiplicity. The sum of zeros of a nonconstant elliptic function is equal to the number of poles there and counted according to their multiplicity. The sum of zeros of a nonconstant elliptic function 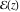 in the fundamental period‐parallelogram in the fundamental period‐parallelogram 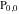 differs from the sum of its poles by a period differs from the sum of its poles by a period 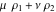 , where , where 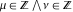 and the values of and the values of 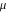 , , 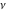 depend on the function depend on the function 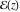 . .
All elliptic functions 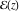 satisfy a common fundamental property, which generalizes addition, duplication, and multiple angle properties for trigonometric and hyperbolic functions (like satisfy a common fundamental property, which generalizes addition, duplication, and multiple angle properties for trigonometric and hyperbolic functions (like 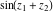 , , 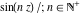 ). It can be formulated as the following: ). It can be formulated as the following:
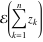 . .
It can also be expressed as an algebraic function of 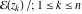 . .
In other words, there exists an irreducible polynomial 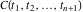 in in 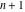 variables with constant coefficients, for which the following relation holds: variables with constant coefficients, for which the following relation holds:
And conversely, among all smooth functions, only elliptic functions and their degenerations have algebraic addition theorems.
The simplest elliptic functions (with order 2) can be divided into two classes:
(1) Functions that at the period‐parallelogram 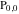 have only a double pole with residue zero (e.g., the Weierstrass elliptic functions have only a double pole with residue zero (e.g., the Weierstrass elliptic functions 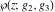 ). ).
(2) Functions that in the period‐parallelogram 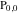 have only two simple poles with residues, which are equal in absolute value but opposite in sign (e.g., Jacobian elliptic functions have only two simple poles with residues, which are equal in absolute value but opposite in sign (e.g., Jacobian elliptic functions 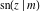 etc.). etc.).
Any elliptic function 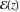 with periods with periods 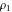 and and 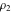 can be expressed as a rational function of the Weierstrassian elliptic functions can be expressed as a rational function of the Weierstrassian elliptic functions 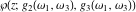 and their derivative and their derivative 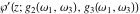 with the same periods with the same periods  . .
The Weierstrass elliptic function 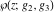 arises as a solution to the following ordinary nonlinear differential equation: arises as a solution to the following ordinary nonlinear differential equation:
Definitions of Weierstrass functions and inverses
The Weierstrass elliptic 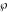 function function 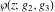 , its derivative , its derivative 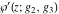 , the Weierstrass sigma function , the Weierstrass sigma function 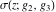 , associated Weierstrass sigma functions , associated Weierstrass sigma functions 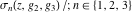 , Weierstrass zeta function , Weierstrass zeta function 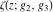 , inverse elliptic Weierstrass , inverse elliptic Weierstrass 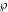 function function 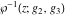 , and generalized inverse Weierstrass , and generalized inverse Weierstrass 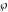 function function 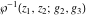 are defined by the following formulas: are defined by the following formulas:
The function 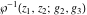 is the unique value of is the unique value of 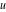 for which for which 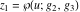 and and 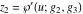 . For the existence of . For the existence of 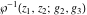 , the values , the values 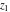 and and 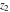 must be related by must be related by 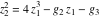 . .
The previous nine functions are typically called Weierstrass elliptic functions. The last two functions are called inverse elliptic Weierstrass functions.
Despite the commonly used naming convention, only the Weierstrass function 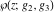 and its derivative and its derivative 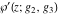 are elliptic functions because only these functions are doubly periodic. The other Weierstrass functions are elliptic functions because only these functions are doubly periodic. The other Weierstrass functions 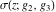 , , 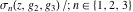 , and , and 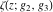 are not elliptic functions because they are only quasi‐periodic functions with respect to are not elliptic functions because they are only quasi‐periodic functions with respect to 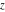 . But historically they are also placed into the class of elliptic functions. . But historically they are also placed into the class of elliptic functions.
The Weierstrass half‐periods 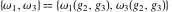 and the invariants and the invariants 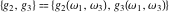 , the Weierstrass , the Weierstrass 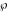 function values at half-periods function values at half-periods 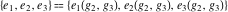 , and the Weierstrass zeta function values at half-periods , and the Weierstrass zeta function values at half-periods 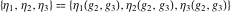 are defined by the following formulas. The description of the Weierstrass functions follows the notations used throughout. The left‐hand sides indicate that are defined by the following formulas. The description of the Weierstrass functions follows the notations used throughout. The left‐hand sides indicate that 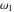 and and 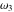 are either independent variables or depend on are either independent variables or depend on 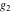 and and 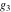 , or vice versa: , or vice versa:
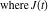 is the Klein invariant modular function, is the Klein invariant modular function, 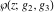 is the Weierstrass elliptic is the Weierstrass elliptic 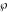 function, and function, and 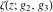 denotes the Weierstrass zeta function. denotes the Weierstrass zeta function.
A quick look at the Weierstrass functions and inverses Here is a quick look at the graphics for the Weierstrass functions and inverses. All of the following graphics use the half-periods 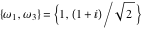 . . The next pair of graphics shows the Weierstrass  function over the complex function over the complex  ‐plane. The double periodicity of the function and the poles of order 2 are clearly visible. ‐plane. The double periodicity of the function and the poles of order 2 are clearly visible. The next pair of graphics shows the derivative of the Weierstrass 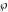 function over the complex function over the complex 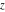 ‐plane. The double periodicity of the function and the poles of order 3 are clearly visible. ‐plane. The double periodicity of the function and the poles of order 3 are clearly visible. The next pair of graphics shows the Weierstrass zeta function over the complex 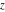 ‐plane. The pseudo‐double periodicity of the function and the poles of order 1 are clearly visible. ‐plane. The pseudo‐double periodicity of the function and the poles of order 1 are clearly visible. The next pair of graphics shows the Weierstrass sigma function over the complex 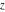 ‐plane. ‐plane. The next three pairs of graphics show the associated Weierstrass sigma functions over the complex 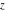 ‐plane. ‐plane. The last pair of graphics shows the inverse of the Weierstrass 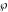 function over the complex function over the complex 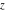 ‐plane. Compared with the direct function, it is relatively structureless. ‐plane. Compared with the direct function, it is relatively structureless.
Connections within the group of Weierstrass functions and inverses and with other function groups
Representations through more general functions
The Weierstrass elliptic 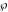 function function 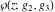 and its inverse and its inverse 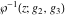 can be represented through the more general hypergeometric Appell can be represented through the more general hypergeometric Appell 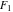 function of two variables by the following formulas: function of two variables by the following formulas:
Representations through related equivalent functions
The Weierstrass functions 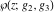 , , 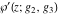 , , 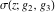 , , 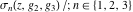 , , 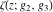 , , 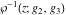 , and , and 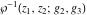 can be represented through some related equivalent functions, for example, through Jacobi functions: can be represented through some related equivalent functions, for example, through Jacobi functions:
where 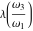 is modular lambda function, or through theta functions: is modular lambda function, or through theta functions:
or through elliptic integrals and the inverse elliptic nome:
Relations to inverse functions
The Weierstrass function 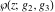 and its derivative and its derivative 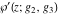 are interconnected with the inverse functions are interconnected with the inverse functions 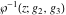 and and 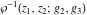 by the following formulas: by the following formulas:
Representations through other Weierstrass functions
Each of the Weierstrass functions 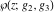 , , 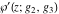 , , 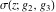 , , 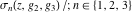 , and , and 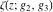 can be expressed through the other Weierstrass functions using numerous formulas, for example: can be expressed through the other Weierstrass functions using numerous formulas, for example:
Note that the Weierstrass functions 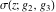 , , 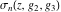 , , 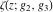 , , 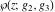 , and , and 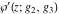 form a chain with respect to differentiation: form a chain with respect to differentiation:
The best-known properties and formulas for Weierstrass functions and inverses
Simple values at zero
The Weierstrass functions 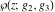 , , 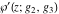 , , 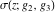 , and , and 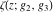 have the following simple values at the origin point: have the following simple values at the origin point:
Specific values for specialized parameter
The Weierstrass functions 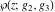 , , 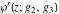 , , 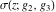 , , 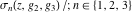 , and , and 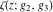 can be represented through elementary functions, when can be represented through elementary functions, when 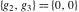 or or 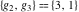 : :
At points 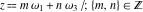 , all Weierstrass functions , all Weierstrass functions 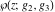 , , 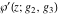 , , 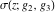 , , 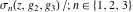 , and , and 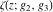 can be equal to zero or can have poles and be equal to can be equal to zero or can have poles and be equal to 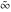 : :
The values of Weierstrass functions 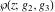 , , 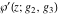 , , 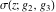 , , 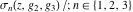 , and , and 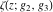 at the points at the points 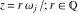 can sometimes be evaluated in closed form: can sometimes be evaluated in closed form:
The Weierstrass functions 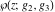 , , 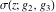 , and , and 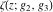 have rather simple values, when have rather simple values, when 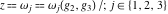 and and 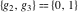 or or 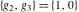 : :
The Weierstrass functions 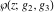 , , 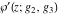 , , 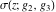 , and , and 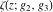 can be represented through elementary functions, when can be represented through elementary functions, when 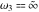 : :
Analyticity
The Weierstrass functions 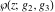 , , 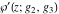 , , 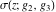 , , 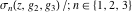 , , 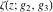 , and , and 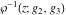 are analytical functions of are analytical functions of 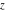 , , 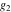 , and , and 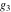 , which are defined in , which are defined in 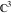 . The inverse Weierstrass function . The inverse Weierstrass function 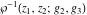 is an analytical function of is an analytical function of 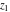 , , 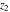 , , 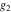 , , 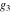 , which is also defined in , which is also defined in  , because , because 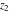 is not an independent variable. is not an independent variable.
Poles and essential singularities
For fixed 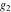 , , 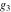 , the Weierstrass functions , the Weierstrass functions 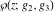 , , 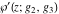 , and , and 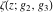 have an infinite set of singular points: have an infinite set of singular points:
(a) 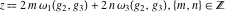 are the poles of order 2 with residues 0 (for are the poles of order 2 with residues 0 (for 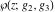 ), of order 3 with residues 0 (for ), of order 3 with residues 0 (for 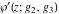 ) and simple poles with residues 1 (for ) and simple poles with residues 1 (for 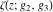 ). ).
(b) 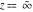 is an essential singular point. is an essential singular point.
For fixed 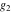 , , 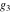 , the Weierstrass functions , the Weierstrass functions 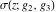 and and 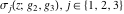 have only one singular point at have only one singular point at 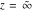 . It is an essential singular point. . It is an essential singular point.
The Weierstrass functions 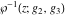 and and 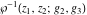 do not have poles and essential singularities with respect to their variables. do not have poles and essential singularities with respect to their variables.
Branch points and branch cuts
For fixed 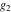 , , 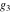 , the Weierstrass functions , the Weierstrass functions 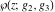 , , 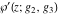 , , 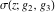 , , 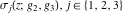 , and , and 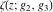 do not have branch points and branch cuts. do not have branch points and branch cuts.
For fixed 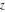 , , 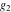 , the inverse Weierstrass function , the inverse Weierstrass function 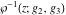 has two branch points: has two branch points: 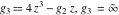 . .
For fixed 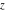 , , 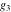 , the inverse Weierstrass function , the inverse Weierstrass function 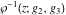 has two branch points: has two branch points: 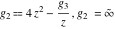 . .
For fixed 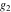 , , 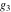 , the inverse Weierstrass function , the inverse Weierstrass function 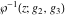 has four branch points: has four branch points: 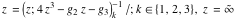 . .
Periodicity
The Weierstrass functions 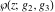 and and 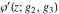 are doubly periodic functions with respect to are doubly periodic functions with respect to 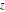 with periods with periods 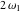 and and 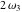 : :
The Weierstrass functions 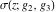 , , 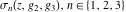 , and , and 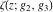 are quasi‐periodic functions with respect to are quasi‐periodic functions with respect to 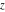 : :
The inverse Weierstrass functions 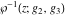 and and 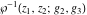 do not have periodicity and symmetry. do not have periodicity and symmetry.
Transformation of half-periods
The Weierstrass functions 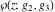 , , 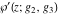 , , 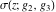 , , 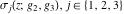 , and , and 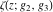 are the invariant functions under the linear transformation of the half‐periods are the invariant functions under the linear transformation of the half‐periods 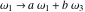 , , 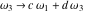 with integer coefficients with integer coefficients 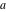 , , 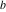 , , 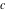 , and , and 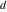 , satisfying restrictions , satisfying restrictions 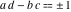 (modular transformations): (modular transformations):
Homogeneity
The Weierstrass functions 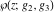 , , 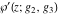 , , 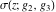 , , 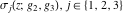 , and , and 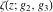 satisfy the following homogeneity type relations: satisfy the following homogeneity type relations:
Parity and symmetry
The Weierstrass functions 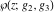 , , 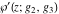 , , 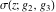 , , 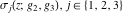 , , 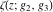 , and , and 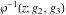 have mirror symmetry: have mirror symmetry:
The Weierstrass functions 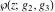 and and 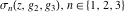 are even functions with respect to are even functions with respect to 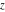 : :
The Weierstrass functions 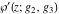 , , 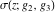 , and , and 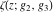 are odd functions with respect to are odd functions with respect to 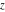 : :
Series representations
The Weierstrass functions 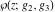 , , 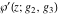 , , 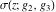 , and , and 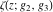 have the following series expansions at the point have the following series expansions at the point 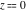 : :
The inverse Weierstrass function 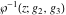 has the following series expansion at the point has the following series expansion at the point 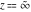 : :
q-series representations
The Weierstrass functions 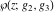 , , 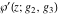 , , 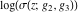 , , 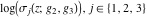 , and , and 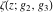 have the following so-called have the following so-called 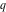 ‐series representations: ‐series representations:
Other series representations
The Weierstrass functions 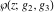 , , 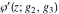 , , 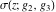 , , 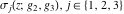 , and , and 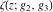 with with 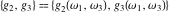 can be represented through series of different forms, for example: can be represented through series of different forms, for example:
Integral representations
The Weierstrass functions and their inverses 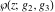 , , 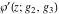 , , 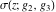 , , 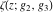 , , 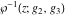 , and , and 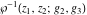 can be represented through the following integrals from elementary or Weierstrass functions: can be represented through the following integrals from elementary or Weierstrass functions:
Product representations
The Weierstrass functions 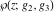 , , 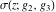 , and , and 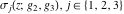 have the following product representations: have the following product representations:
q-product representations
The Weierstrass functions 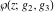 , , 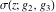 , and , and 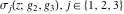 can be represented as so-called can be represented as so-called 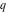 ‐products by the following formulas: ‐products by the following formulas:
Transformations
The Weierstrass functions 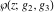 , , 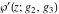 , , 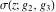 , , 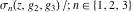 , and , and 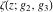 satisfy numerous relations that can provide transformations of its arguments. One of these transformations simplifies argument satisfy numerous relations that can provide transformations of its arguments. One of these transformations simplifies argument 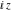 to to 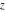 , for example: , for example:
Other transformations are described by so-called addition formulas:
Half‐angle formulas provide one more type of transformation, for example:
The Weierstrass functions 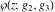 , , 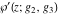 , , 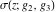 , and , and 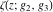 satisfy the following double-angle formulas: satisfy the following double-angle formulas:
These formulas can be expanded on triple angle formulas, for example:
Generally the following multiple angle formulas take place:
Sometimes transformations have a symmetrical character, which includes operations like determinate, for example:
A special class of transformation includes the simplification of Weierstrass functions 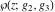 , , 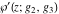 , , 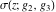 , , 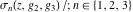 , and , and 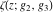 with invariants with invariants 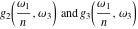 , where , where 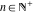 , for example: , for example:
Identities
The Weierstrass functions satisfy numerous functional identities, for example:
Representations of derivatives
The first two derivatives of all Weierstrass functions 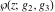 , , 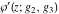 , , 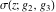 , , 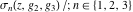 , and , and 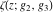 , and their inverses , and their inverses 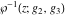 and and 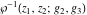 with respect to variable with respect to variable 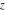 can also be expressed through Weierstrass functions: can also be expressed through Weierstrass functions:
The first derivatives of Weierstrass functions 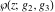 , , 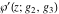 , , 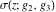 , and , and 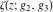 with respect to parameter with respect to parameter 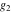 can also be expressed through Weierstrass functions by the following formulas: can also be expressed through Weierstrass functions by the following formulas:
The first derivatives of Weierstrass functions 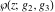 , , 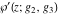 , , 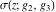 , and , and 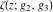 with respect to parameter with respect to parameter 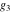 can also be expressed through Weierstrass functions by the following formulas: can also be expressed through Weierstrass functions by the following formulas:
Weierstrass invariants 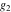 and and 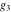 can be expressed as functions of half-periods can be expressed as functions of half-periods 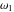 and and 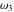 . This property allows obtaining the following formulas for the first derivatives of Weierstrass functions . This property allows obtaining the following formulas for the first derivatives of Weierstrass functions 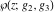 , , 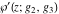 , , 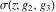 , and , and 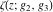 with respect to half-period with respect to half-period 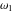 : :
Similar formulas take place for the first derivatives of Weierstrass functions 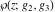 , , 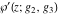 , , 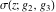 , and , and 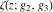 with respect to half-period with respect to half-period 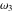 : :
The 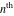 derivatives of all Weierstrass functions derivatives of all Weierstrass functions 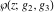 , , 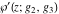 , , 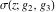 , , 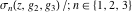 , , 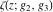 , and their inverses , and their inverses 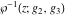 and and 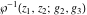 with respect to variable with respect to variable 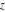 can be represented by the following formulas: can be represented by the following formulas:
Integration
The indefinite integrals of Weierstrass functions 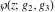 , , 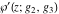 , , 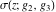 , and , and 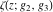 with respect to variable with respect to variable 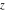 can be expressed by the following formulas: can be expressed by the following formulas:
Summation
Finite and infinite sums including Weierstrass functions can sometimes be evaluated in closed forms, for example:
Differential equations
The Weierstrass functions 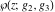 , , 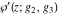 , , 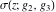 , , 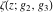 , and their inverses , and their inverses 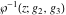 and and 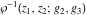 satisfy the following nonlinear differential equations: satisfy the following nonlinear differential equations:
The Weierstrass functions 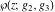 , , 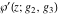 , , 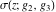 , and , and 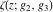 are the special solutions of the corresponding partial differential equations: are the special solutions of the corresponding partial differential equations:
Applications of Weierstrass functions and inverses
Applications of Weierstrass functions include integrable nonlinear differential equations, motion in cubic and quartic potentials, description of the movement of a spherical pendulum, and construction of minimal surfaces.
|