|
Definitions of Weierstrass functions and inverses
The Weierstrass elliptic 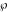 function function 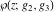 , its derivative , its derivative 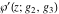 , the Weierstrass sigma function , the Weierstrass sigma function 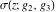 , associated Weierstrass sigma functions , associated Weierstrass sigma functions 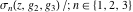 , Weierstrass zeta function , Weierstrass zeta function 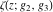 , inverse elliptic Weierstrass , inverse elliptic Weierstrass 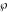 function function 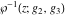 , and generalized inverse Weierstrass , and generalized inverse Weierstrass 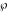 function function 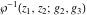 are defined by the following formulas: are defined by the following formulas:
The function 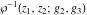 is the unique value of is the unique value of 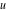 for which for which 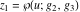 and and 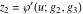 . For the existence of . For the existence of 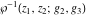 , the values , the values 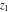 and and 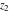 must be related by must be related by 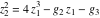 . .
The previous nine functions are typically called Weierstrass elliptic functions. The last two functions are called inverse elliptic Weierstrass functions.
Despite the commonly used naming convention, only the Weierstrass function 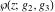 and its derivative and its derivative 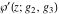 are elliptic functions because only these functions are doubly periodic. The other Weierstrass functions are elliptic functions because only these functions are doubly periodic. The other Weierstrass functions 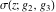 , , 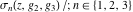 , and , and 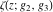 are not elliptic functions because they are only quasi‐periodic functions with respect to are not elliptic functions because they are only quasi‐periodic functions with respect to 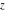 . But historically they are also placed into the class of elliptic functions. . But historically they are also placed into the class of elliptic functions.
The Weierstrass half‐periods 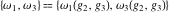 and the invariants and the invariants 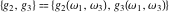 , the Weierstrass , the Weierstrass 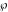 function values at half-periods function values at half-periods 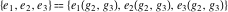 , and the Weierstrass zeta function values at half-periods , and the Weierstrass zeta function values at half-periods 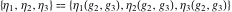 are defined by the following formulas. The description of the Weierstrass functions follows the notations used throughout. The left‐hand sides indicate that are defined by the following formulas. The description of the Weierstrass functions follows the notations used throughout. The left‐hand sides indicate that 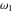 and and 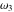 are either independent variables or depend on are either independent variables or depend on 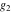 and and 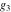 , or vice versa: , or vice versa:
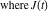 is the Klein invariant modular function, is the Klein invariant modular function, 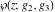 is the Weierstrass elliptic is the Weierstrass elliptic 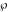 function, and function, and 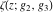 denotes the Weierstrass zeta function. denotes the Weierstrass zeta function.
|