|
The Weierstrass elliptic 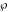 function function 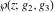 and its inverse and its inverse 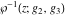 can be represented through the more general hypergeometric Appell can be represented through the more general hypergeometric Appell 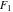 function of two variables by the following formulas: function of two variables by the following formulas:
The Weierstrass functions 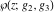 , , 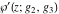 , , 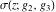 , , 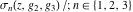 , , 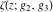 , , 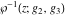 , and , and 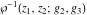 can be represented through some related equivalent functions, for example, through Jacobi functions: can be represented through some related equivalent functions, for example, through Jacobi functions:
where 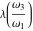 is modular lambda function, or through theta functions: is modular lambda function, or through theta functions:
or through elliptic integrals and the inverse elliptic nome:
The Weierstrass function 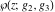 and its derivative and its derivative 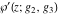 are interconnected with the inverse functions are interconnected with the inverse functions 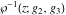 and and 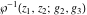 by the following formulas: by the following formulas:
Each of the Weierstrass functions 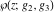 , , 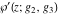 , , 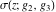 , , 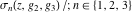 , and , and 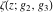 can be expressed through the other Weierstrass functions using numerous formulas, for example: can be expressed through the other Weierstrass functions using numerous formulas, for example:
Note that the Weierstrass functions 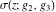 , , 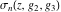 , , 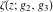 , , 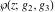 , and , and 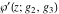 form a chain with respect to differentiation: form a chain with respect to differentiation:
|