|
Connections within the group of incomplete elliptic integrals and with other function groups
Representations through more general functions
The incomplete elliptic integrals 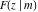 , , 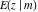 , , 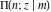 , and , and 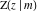 can be represented through more general functions. Through the hypergeometric Appell can be represented through more general functions. Through the hypergeometric Appell 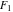 function of two variables: function of two variables:
Through the generalized hypergeometric function of two variables:
Through elliptic theta functions, for example:
Through inverse Jacobi elliptic functions, for example:
Through Weierstrass elliptic functions and inverse elliptic nome 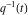 , for example: , for example:
Through some elliptic‐type functions, for example:
Representations through related functions
The incomplete elliptic integrals 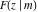 , , 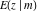 , , 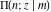 , and , and 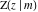 can be represented through some related functions, for example: can be represented through some related functions, for example:
Relations to inverse functions
The incomplete elliptic integral 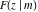 is related to the Jacobi amplitude by the following formulas, which demonstrate that the Jacobi amplitude is within a restricted domain, the inverse function of elliptic integral is related to the Jacobi amplitude by the following formulas, which demonstrate that the Jacobi amplitude is within a restricted domain, the inverse function of elliptic integral 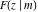 : :
Representations through other incomplete elliptic integrals
The incomplete elliptic integrals 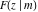 , , 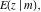 and and 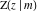 can be represented through incomplete elliptic integral can be represented through incomplete elliptic integral 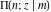 by the following formulas: by the following formulas:
|