|
For real values of argument 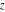 , the values of the probability integrals , the values of the probability integrals 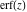 , , 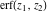 , , 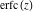 , and , and 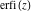 are real. For real arguments are real. For real arguments 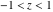 , the values of the inverse error function , the values of the inverse error function 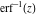 are real; for real arguments are real; for real arguments 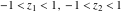 , the values of the inverse of the generalized error function , the values of the inverse of the generalized error function 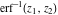 are real; and for real arguments are real; and for real arguments  , the values of the inverse complementary error function , the values of the inverse complementary error function 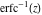 are real. are real.
The probability integrals 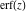 , , 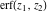 , , 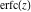 , and , and 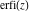 , and their inverses , and their inverses 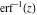 , , 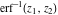 , and , and 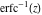 have simple values for zero or unit arguments: have simple values for zero or unit arguments:
The probability integrals 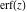 , , 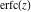 , and , and 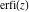 have simple values at infinity: have simple values at infinity:
In cases when 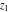 or or 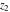 is equal to is equal to 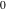 or or 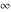 , the generalized error function , the generalized error function 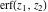 and its inverse and its inverse 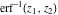 can be expressed through the probability integrals can be expressed through the probability integrals 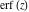 , , 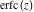 , or their inverses by the following formulas: , or their inverses by the following formulas:
The probability integrals 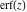 , , 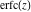 , and , and 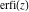 , and their inverses , and their inverses 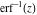 , and , and 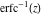 are defined for all complex values of are defined for all complex values of 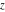 , and they are analytical functions of , and they are analytical functions of 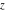 over the whole complex over the whole complex 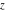 ‐plane. The probability integrals ‐plane. The probability integrals 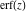 , , 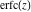 , and , and  are entire functions with an essential singular point at are entire functions with an essential singular point at 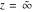 , and they do not have branch cuts or branch points. , and they do not have branch cuts or branch points.
The generalized error function 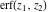 is an analytical function of is an analytical function of 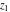 and and 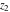 , which is defined in , which is defined in 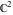 . For fixed . For fixed 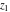 , it is an entire function of , it is an entire function of 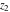 . For fixed . For fixed 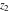 , it is an entire function of , it is an entire function of 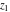 . It does not have branch cuts or branch points.
The inverse of the generalized error function . It does not have branch cuts or branch points.
The inverse of the generalized error function 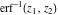 is an analytical function of is an analytical function of  and and  , which is defined in , which is defined in 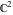 . .
The probability integrals 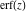 , , 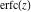 , and , and 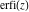 have only one singular point at have only one singular point at 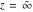 . It is an essential singular point. . It is an essential singular point.
The generalized error function 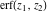 has singular points at has singular points at 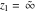 and and 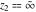 . They are essential singular points. . They are essential singular points.
The probability integrals 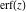 , , 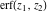 , , 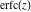 , and , and 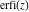 , and their inverses , and their inverses  , , 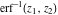 , and , and 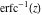 do not have periodicity. do not have periodicity.
The probability integrals 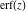 , ,  , and , and 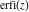 are odd functions and have mirror symmetry: are odd functions and have mirror symmetry:
The generalized error function 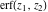 has permutation symmetry: has permutation symmetry:
The complementary error function 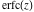 has mirror symmetry: has mirror symmetry:
The probability integrals 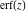 , , 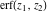 , ,  , and , and 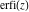 , and their inverses , and their inverses 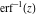 and and 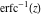 have the following series expansions: have the following series expansions:
The series for functions  , , 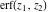 , , 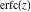 , and , and 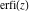 converge for all complex values of their arguments. converge for all complex values of their arguments.
Interestingly, closed-form expressions for the truncated version of the Taylor series at the origin can be expressed through generalized hypergeometric function 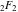 , for example: , for example:
The asymptotic behavior of the probability integrals 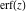 , , 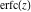 , and , and 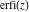 can be described by the following formulas (only the main terms of the asymptotic expansion are given): can be described by the following formulas (only the main terms of the asymptotic expansion are given):
The previous formulas are valid in any direction approaching infinity (z∞). In particular cases, these formulas can be simplified to the following relations:
The probability integrals 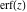 , , 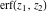 , , 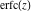 , and , and  can also be represented through the following equivalent integrals: can also be represented through the following equivalent integrals:
The symbol 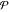 in the preceding integral means that the integral evaluates as the Cauchy principal value: in the preceding integral means that the integral evaluates as the Cauchy principal value: 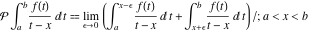 . .
If the arguments of the probability integrals  , , 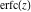 , and , and 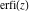 contain square roots, the arguments can sometimes be simplified: contain square roots, the arguments can sometimes be simplified:
The derivative of the probability integrals 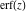 , , 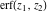 , , 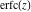 , and , and 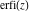 , and their inverses , and their inverses  , , 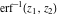 , and , and 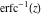 have simple representations through elementary functions: have simple representations through elementary functions:
The symbolic 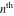 -order derivatives from the probability integrals -order derivatives from the probability integrals 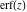 , , 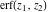 , , 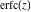 , and , and 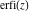 have the following simple representations through the regularized generalized hypergeometric function have the following simple representations through the regularized generalized hypergeometric function  : :
But the symbolic 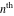 -order derivatives from the inverse probability integrals -order derivatives from the inverse probability integrals 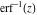 , ,  , and , and 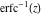 have very complicated structures in which the regularized generalized hypergeometric function have very complicated structures in which the regularized generalized hypergeometric function 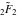 appears in the multidimensional sums, for example: appears in the multidimensional sums, for example:
The probability integrals  , , 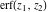 , , 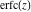 , and , and 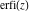 satisfy the following second-order linear differential equations: satisfy the following second-order linear differential equations:
where 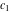 and and 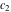 are arbitrary constants. are arbitrary constants.
The inverses of the probability integrals 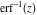 , ,  , and , and 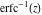 satisfy the following ordinary second-order nonlinear differential equations: satisfy the following ordinary second-order nonlinear differential equations:
|