|
Connections within the group of probability integrals and inverses and with other function groups
Representations through more general functions
The probability integrals 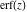 , , 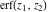 , , 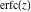 , and , and 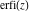 are the particular cases of two more general functions: hypergeometric and Meijer G functions. are the particular cases of two more general functions: hypergeometric and Meijer G functions.
For example, they can be represented through the confluent hypergeometric functions 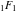 and and 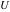 : :
Representations of the probability integrals 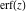 , , 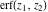 , , 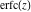 , and , and 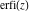 through classical Meijer G functions are rather simple: through classical Meijer G functions are rather simple:
The factor 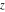 in the last four formulas can be removed by changing the classical Meijer G functions to the generalized one: in the last four formulas can be removed by changing the classical Meijer G functions to the generalized one:
The probability integrals 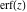 , , 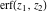 , , 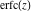 , and , and 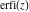 are the particular cases of the incomplete gamma function, regularized incomplete gamma function, and exponential integral are the particular cases of the incomplete gamma function, regularized incomplete gamma function, and exponential integral 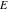 : :
Representations through related equivalent functions
The probability integrals 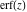 , , 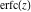 , and , and 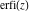 can be represented through Fresnel integrals by the following formulas: can be represented through Fresnel integrals by the following formulas:
Representations through other probability integrals and inverses
The probability integrals and their inverses 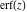 , , 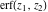 , , 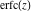 , , 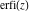 , , 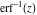 , , 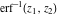 , and , and 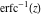 are interconnected by the following formulas: are interconnected by the following formulas:
|