|
Connections within the group of gamma functions and with other function groups
Representations through more general functions
The incomplete gamma functions 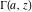 , ,  , ,  , and , and  are particular cases of the more general hypergeometric and Meijer G functions. are particular cases of the more general hypergeometric and Meijer G functions.
For example, they can be represented through hypergeometric functions 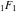 and and 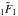 or the Tricomi confluent hypergeometric function or the Tricomi confluent hypergeometric function 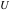 : :
These functions also have rather simple representations in terms of classical Meijer G functions:
The log‐gamma function 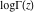 can be expressed through polygamma and zeta functions by the following formulas: can be expressed through polygamma and zeta functions by the following formulas:
Representations through related equivalent functions
The gamma functions 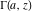 , , 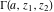 , , 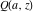 , and , and 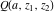 can be represented using the related exponential integral can be represented using the related exponential integral 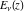 by the following formulas: by the following formulas:
Relations to inverse functions
The gamma functions 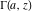 , , 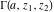 , , 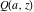 , and , and 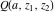 are connected with the inverse of the regularized incomplete gamma function are connected with the inverse of the regularized incomplete gamma function 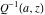 and the inverse of the generalized regularized incomplete gamma function and the inverse of the generalized regularized incomplete gamma function 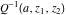 by the following formulas: by the following formulas:
Representations through other gamma functions
The gamma functions 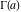 , , 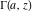 , , 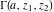 , , 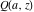 , ,  , and , and  are connected with each other by the formulas: are connected with each other by the formulas:
|