|
For real values of parameter 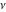 and positive argument and positive argument 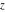 , the values of the exponential integral , the values of the exponential integral 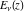 are real (or infinity). For real values of argument are real (or infinity). For real values of argument 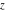 , the values of the exponential integral , the values of the exponential integral 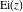 , the sine integral , the sine integral 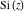 , and the hyperbolic sine integral , and the hyperbolic sine integral 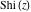 are real. For real positive values of argument are real. For real positive values of argument 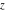 , the values of the logarithmic integral , the values of the logarithmic integral 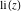 , the cosine integral , the cosine integral 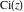 , and the hyperbolic cosine integral , and the hyperbolic cosine integral 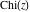 are real. are real.
The exponential integrals have rather simple values for argument 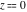 : :
If the parameter 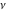 equals equals 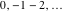 , the exponential integral , the exponential integral 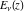 can be expressed through an exponential function multiplied by a simple rational function. If the parameter can be expressed through an exponential function multiplied by a simple rational function. If the parameter 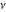 equals equals 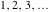 , the exponential integral , the exponential integral 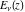 can be expressed through the exponential integral can be expressed through the exponential integral 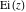 , and the exponential and logarithmic functions: , and the exponential and logarithmic functions:
The previous formulas are the particular cases of the following general formula:
If the parameter 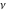 equals equals 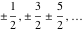 , the exponential integral , the exponential integral 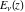 can be expressed through the probability integral can be expressed through the probability integral 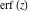 , and the exponential and power functions, for example: , and the exponential and power functions, for example:
The previous formulas can be generalized by the following general representation of this class of particular cases:
The exponential integrals 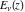 , , 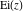 , , 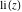 , , 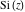 , , 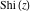 , , 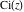 , and , and 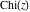 are defined for all complex values of the parameter are defined for all complex values of the parameter 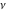 and the variable and the variable 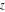 . The function . The function 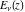 is an analytical functions of is an analytical functions of 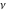 and and 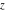 over the whole complex over the whole complex 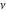 ‐ and ‐ and 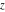 ‐planes excluding the branch cut on the ‐planes excluding the branch cut on the 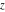 ‐plane. For fixed ‐plane. For fixed 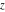 , the exponential integral , the exponential integral 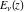 is an entire function of is an entire function of 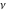 . The sine integral . The sine integral 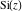 and the hyperbolic sine integral and the hyperbolic sine integral 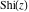 are entire functions of are entire functions of 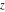 . .
For fixed 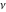 , the function , the function 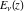 has an essential singularity at has an essential singularity at 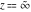 . At the same time, the point . At the same time, the point 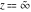 is a branch point for generic is a branch point for generic 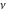 . For fixed . For fixed 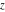 , the function , the function 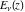 has only one singular point at has only one singular point at 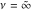 . It is an essential singular point. . It is an essential singular point.
The exponential integral 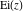 , the cosine integral , the cosine integral 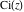 , and the hyperbolic cosine integral , and the hyperbolic cosine integral 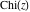 have an essential singularity at have an essential singularity at 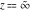 . .
The function 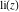 does not have poles and essential singularities. does not have poles and essential singularities.
The sine integral 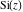 and the hyperbolic sine integral and the hyperbolic sine integral 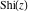 have an essential singularity at have an essential singularity at 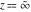 . .
For fixed 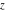 , the function , the function 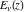 does not have branch points and branch cuts. does not have branch points and branch cuts.
For fixed 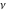 , not being a nonpositive integer, the function , not being a nonpositive integer, the function 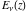 has two branch points has two branch points 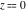 and and 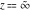 , and branch cuts along the interval , and branch cuts along the interval 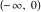 . At the same time, the point . At the same time, the point 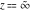 is an essential singularity for this function. is an essential singularity for this function.
The exponential integral 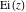 , the cosine integral , the cosine integral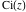 , and the hyperbolic cosine integral , and the hyperbolic cosine integral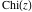 have two branch points have two branch points 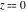 and and 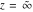 . .
The function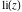 has three branch points has three branch points 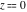 , , 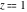 , and , and 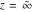 . .
The sine integral 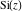 and hyperbolic sine integral and hyperbolic sine integral 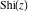 do not have branch points or branch cuts. do not have branch points or branch cuts.
For fixed 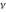 , not being a nonpositive integer, the function , not being a nonpositive integer, the function 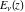 is a single‐valued function on the is a single‐valued function on the 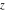 ‐plane cut along the interval ‐plane cut along the interval 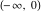 , where it is continuous from above: , where it is continuous from above:
The function 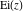 is a single‐valued function on the is a single‐valued function on the 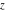 ‐plane cut along the interval ‐plane cut along the interval 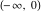 , where it has discontinuities from both sides: , where it has discontinuities from both sides:
The function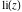 is a single‐valued function on the is a single‐valued function on the 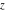 ‐plane cut along the interval ‐plane cut along the interval 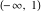 . It is continuous from above along the interval . It is continuous from above along the interval 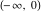 and it has discontinuities from both sides along the interval and it has discontinuities from both sides along the interval 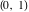 : :
The cosine integral 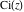 and hyperbolic cosine integral and hyperbolic cosine integral 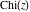 are single‐valued functions on the are single‐valued functions on the 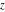 ‐plane cut along the interval ‐plane cut along the interval 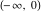 where they are continuous from above: where they are continuous from above:
From below, these functions have discontinuity that are described by the formulas:
The exponential integrals 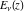 , , 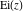 , , 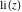 , , 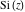 , , 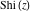 , , 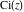 , and , and 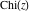 do not have periodicity. do not have periodicity.
The exponential integral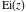 has mirror symmetry: has mirror symmetry:
The sine integral 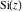 and the hyperbolic sine integral and the hyperbolic sine integral 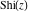 are odd functions and have mirror symmetry: are odd functions and have mirror symmetry:
The exponential integral 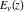 , logarithmic integral , logarithmic integral 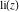 , cosine integral , cosine integral 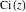 , and hyperbolic cosine integral , and hyperbolic cosine integral 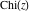 have mirror symmetry (except on the branch cut interval (-∞, 0)): have mirror symmetry (except on the branch cut interval (-∞, 0)):
The exponential integrals 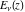 , , 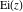 , , 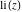 , , 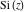 , , 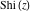 , , 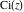 , and , and 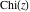 have the following series expansions through series that converge on the whole have the following series expansions through series that converge on the whole 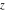 ‐plane: ‐plane:
Interestingly, closed‐form expressions for the truncated version of the Taylor series at the origin can be expressed through the generalized hypergeometric function 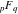 , for example: , for example:
The asymptotic behavior of the exponential integrals 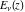 , , 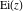 , , 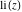 , , 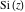 , , 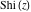 , , 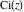 , and , and 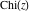 can be described by the following formulas (only the main terms of the asymptotic expansions are given): can be described by the following formulas (only the main terms of the asymptotic expansions are given):
The previous formulas are valid in any direction of approaching point 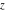 to infinity (z∞). In particular cases, these formulas can be simplified to the following relations: to infinity (z∞). In particular cases, these formulas can be simplified to the following relations:
The exponential integrals 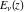 , , 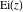 , , 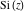 , and , and 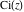 can also be represented through the following equivalent integrals: can also be represented through the following equivalent integrals:
The symbol 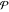 in the second and third integrals means that these integrals evaluate as the Cauchy principal value of the singular integral: in the second and third integrals means that these integrals evaluate as the Cauchy principal value of the singular integral:
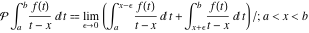 . .
The arguments of the exponential integrals 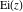 , , 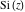 , , 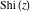 , , 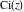 , and , and 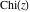 that contain square roots can sometimes be simplified: that contain square roots can sometimes be simplified:
The exponential integral 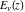 satisfies the following recurrence identities: satisfies the following recurrence identities:
All of the preceding formulas can be generalized to the following recurrence identities with a jump of length 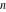 : :
The derivative of the exponential integral 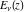 with respect to the variable with respect to the variable 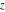 has a simple representation through itself, but with a different parameter: has a simple representation through itself, but with a different parameter:
The derivative of the exponential integral 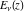 by its parameter by its parameter 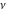 can be represented through the regularized hypergeometric function can be represented through the regularized hypergeometric function 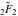 : :
The derivatives of the other exponential integrals 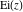 , , 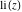 , , 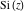 , , 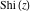 , , 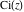 , and , and 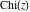 have simple representations through simple elementary functions: have simple representations through simple elementary functions:
The symbolic 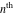 -order derivatives with respect to the variable -order derivatives with respect to the variable 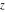 of all exponential integrals of all exponential integrals 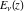 , , 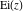 , , 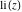 , , 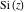 , , 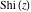 , , 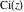 , and , and 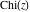 have the following representations: have the following representations:
The exponential integrals 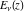 , , 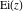 , , 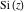 , , 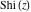 , , 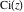 , and , and 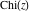 satisfy the following linear differential equations of second or third orders: satisfy the following linear differential equations of second or third orders:
where 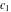 , , 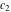 , and , and 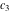 are arbitrary constants. are arbitrary constants.
The logarithmic integral 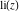 satisfies the following ordinary second-order nonlinear differential equation: satisfies the following ordinary second-order nonlinear differential equation:
|